卷积神经网络复杂度分析
Categories: CNN_Deploy
前言
现阶段的轻量级模型 MobileNet/ShuffleNet 系列、CSPNet、RepVGG、VoVNet 等都必须依赖于于具体的计算平台(如 CPU/GPU/ASIC 等)才能更完美的发挥网络架构。
1,计算平台主要有两个指标:算力 $\pi $和 带宽 $\beta $。
- 算力:计算平台每秒完成的最大浮点运算次数,单位是
FLOPS - 带宽:计算平台一次每秒最多能搬运多少数据(每秒能完成的内存交换量),单位是
Byte/s。
计算强度上限 $I_{max}$,上面两个指标相除得到计算平台的计算强度上限。AI 是衡量从内存加载或存储的每个字节完成了多少操作
这里所说的“内存”是广义上的内存。对于
CPU而言指的就是真正的内存(RAM);而对于GPU则指的是显存。
2,和计算平台的两个指标相呼应,模型有两个反馈速度的间接指标:计算量 FLOPs 和访存量 MAC。
- 计算量(FLOPs):指的是输入单个样本(一张图像),模型完成一次前向传播所发生的浮点运算次数,即模型的时间复杂度,单位是
FLOPs。 - 访存量(MAC):指的是输入单个样本(一张图像),模型完成一次前向传播所发生的内存交换总量,即模型的空间复杂度,单位是
Byte,因为 CNN 模型的权重类型通常为float32,所以一般需要乘以4。CNN网络中每个网络层MAC的计算分为读输入feature map大小、权重大小(DDR读)和写输出feature map大小(DDR写)三部分。 - 模型的计算强度 $I$ :$I = \frac{FLOPs}{MAC}$,即计算量除以访存量后的值,表示此模型在计算过程中,每
Byte内存交换到底用于进行多少次浮点运算。单位是FLOPs/Byte。可以看到,模型计算强度越大,其内存使用效率越高。 - 模型的理论性能 $P$ :我们最关心的指标,即模型在计算平台上所能达到的每秒浮点运算次数(理论值)。单位是
FLOPS or FLOP/s。Roof-line Model给出的就是计算这个指标的方法。
一 模型计算量分析
终端设备上运行深度学习算法需要考虑内存和算力的需求,因此需要进行模型复杂度分析,涉及到模型计算量(时间/计算复杂度)和模型参数量(空间复杂度)分析。
为了分析模型计算复杂度,一个广泛采用的度量方式是模型推断时浮点运算的次数 (FLOPs),即模型理论计算量,但是,它是一个间接的度量,是对我们真正关心的直接度量比如速度或者时延的一种近似估计。
本文的卷积核尺寸假设为为一般情况,即正方形,长宽相等都为 K。
FLOPs:floating point operations 指的是浮点运算次数,理解为计算量,可以用来衡量算法/模型时间的复杂度。FLOPS:(全部大写),Floating-point Operations Per Second,每秒所执行的浮点运算次数,理解为计算速度,是一个衡量硬件性能/模型速度的指标。MACCs:multiply-accumulate operations,乘-加操作次数,MACCs大约是 FLOPs 的一半。将 $w[0]*x[0] + …$ 视为一个乘法累加或1个MACC。
注意相同 FLOPs 的两个模型其运行速度是会相差很多的,因为影响模型运行速度的两个重要因素只通过 FLOPs 是考虑不到的,比如 MAC(Memory Access Cost)和网络并行度;二是具有相同 FLOPs 的模型在不同的平台上可能运行速度不一样。
注意,网上很多文章将 MACCs 与 MACC 概念搞混,我猜测可能是机器翻译英文文章不准确的缘故,可以参考此链接了解更多。需要指出的是,现有很多硬件都将乘加运算作为一个单独的指令。
卷积层 FLOPs 计算:
卷积操作本质上是个线性运算,假设卷积核大小相等且为 $K$。这里给出的公式写法是为了方便理解,大多数时候为了方便记忆,会写成比如 $MACCs = H \times W \times K^2 \times C_i \times C_o$。
- $FLOPs=(2\times C_i\times K^2-1)\times H\times W\times C_o$(不考虑bias)
- $FLOPs=(2\times C_i\times K^2)\times H\times W\times C_o$(考虑bias)
- $MACCs=(C_i\times K^2)\times H\times W\times C_o$(考虑bias)
$C_i$ 为输入特征图通道数,$K$ 为过卷积核尺寸,$H,W,C_o$ 为输出特征图的高,宽和通道数。二维卷积过程如下图所示:
二维卷积是一个相当简单的操作:从卷积核开始,这是一个小的权值矩阵。这个卷积核在 2 维输入数据上「滑动」,对当前输入的部分元素进行矩阵乘法,然后将结果汇为单个输出像素。
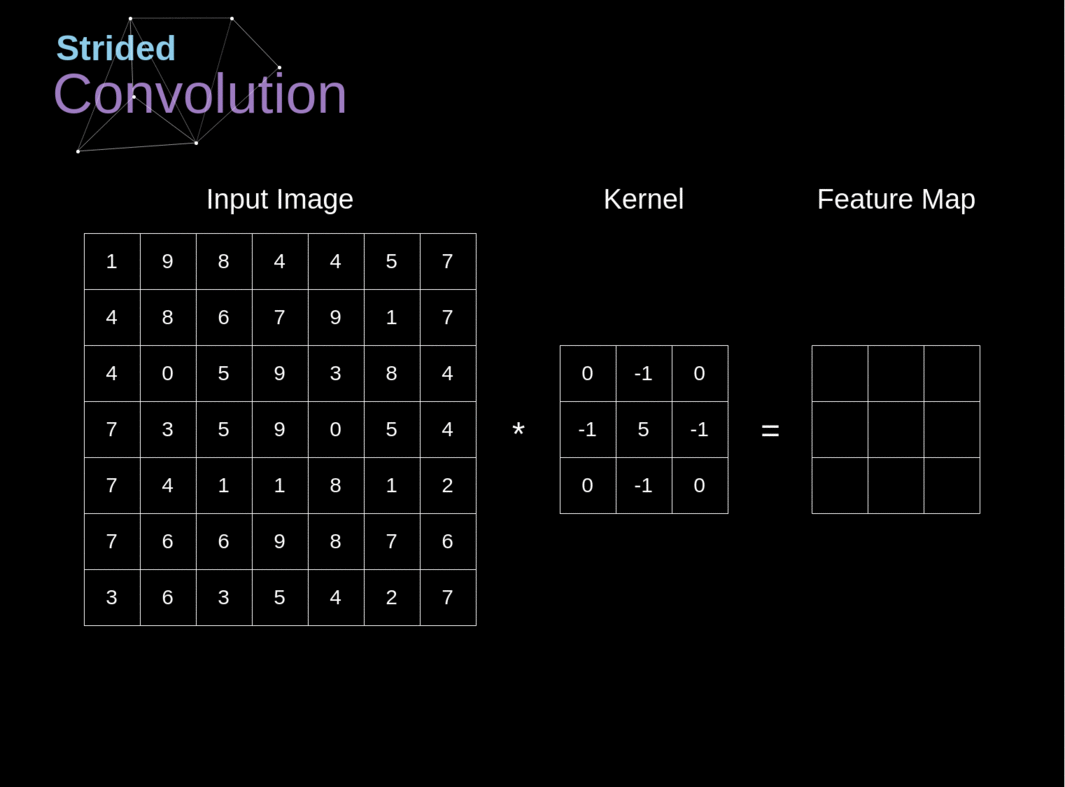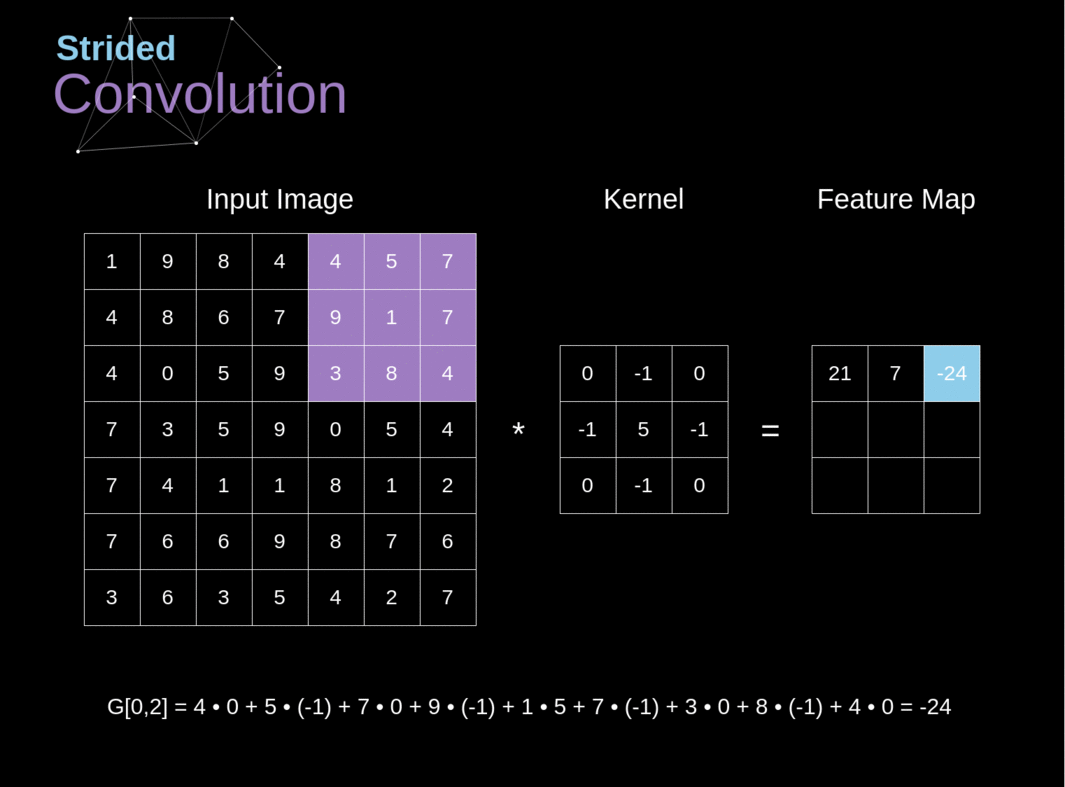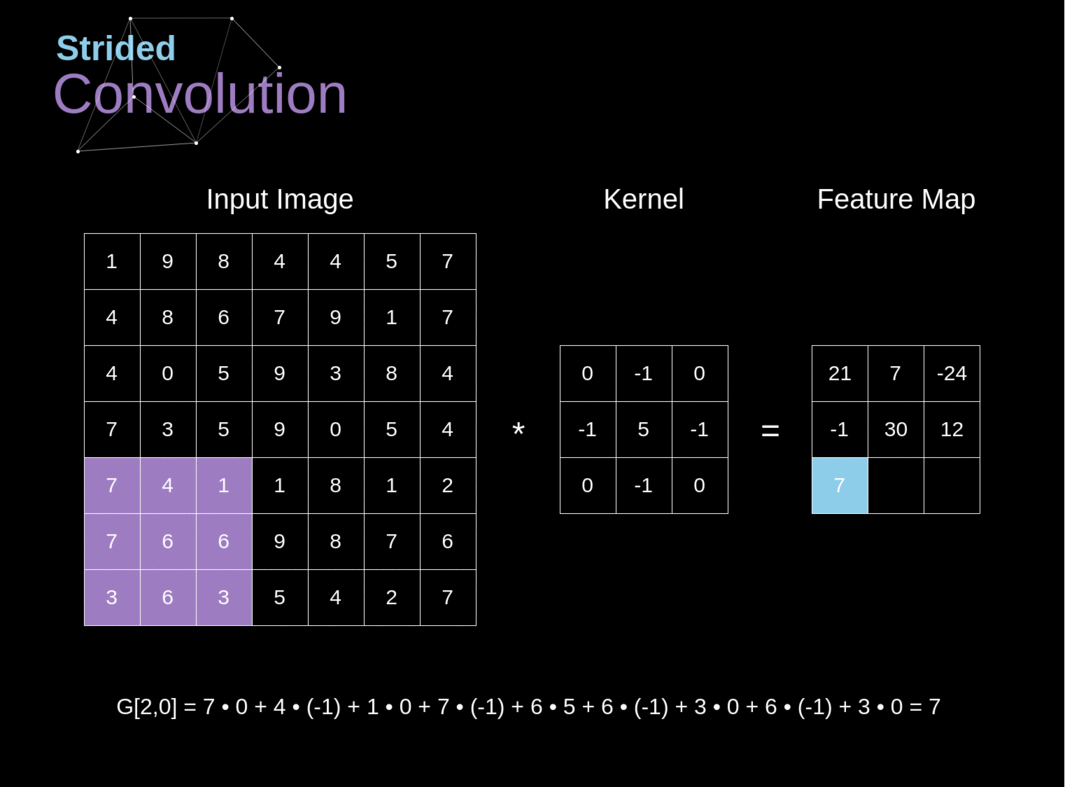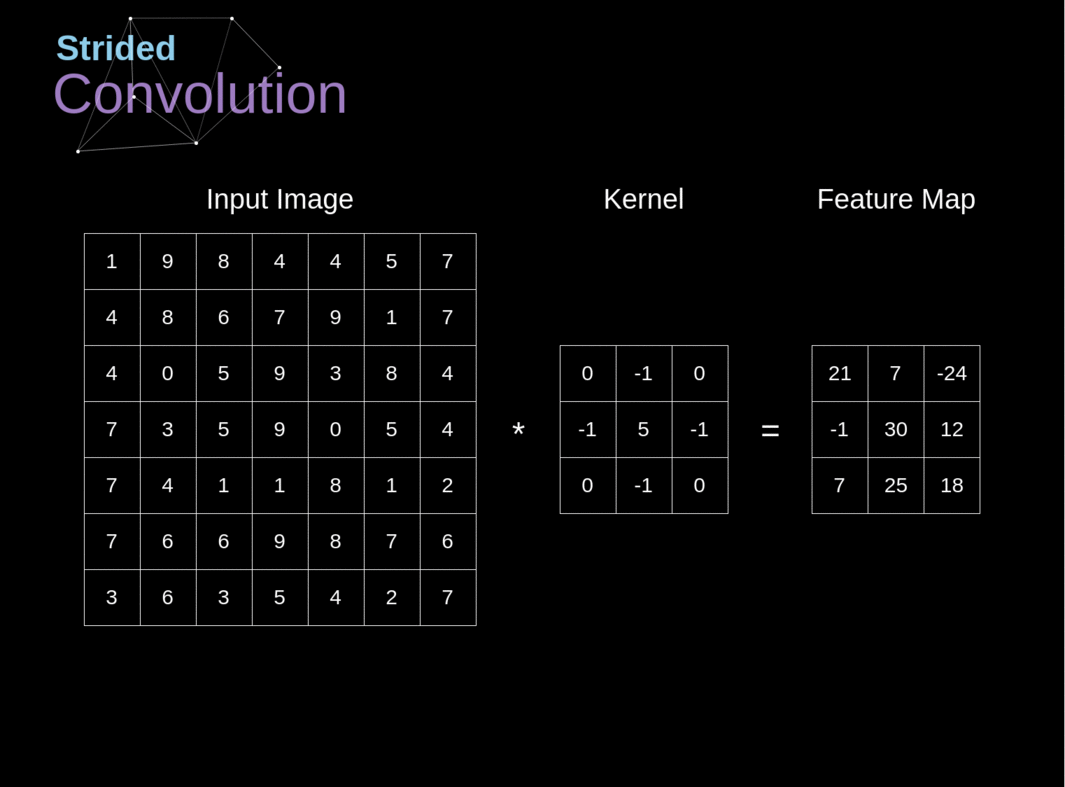
图片来源 Multi-Label Classification and Class Activation Map on Fashion-MNIST。
公式解释如下:
理解 FLOPs 的计算公式分两步。括号内是第一步,即先计算出output feature map 的一个 pixel,然后再乘以 $H\times W\times C_o$,从而拓展到整个 output feature map。括号内的部分又可以分为两步:$(2\times C_i\times K^2-1)=(C_i\times K^2) + (C_i\times K^2-1)$。第一项是乘法运算次数,第二项是加法运算次数,因为 $n$ 个数相加,要加 $n-1$次,所以不考虑 bias 的情况下,会有一个 -1,如果考虑 bias,刚好中和掉,括号内变为$(2\times C_i\times K^2)$。
所以卷积层的 $FLOPs=(2\times C_{i}\times K^2-1)\times H\times W\times C_o$ ($C_i$ 为输入特征图通道数,$K$ 为过滤器尺寸,$H, W, C_o$为输出特征图的高,宽和通道数)。
全连接层的 FLOPs 计算:
假设 $I$ 是输入层的维度,$O$ 是输出层的维度。
- 不考虑 bias,全连接层的 $FLOPs = (I + I -1) \times O = (2I − 1)O$
- 考虑 bias,全连接层的 $FLOPs = (I + I -1) \times O + O = (2\times I)\times O$
1.1 计算利用率(Utilization)
在这种情况下,利用率(Utilization)是可以有效地用于实际工作负载的芯片的原始计算能力的百分比。深度学习和神经网络使用相对数量较少的计算原语(computational primitives),而这些数量很少的计算原语却占用了大部分计算时间。矩阵乘法(MM)和转置是基本操作。MM 由乘法累加(MAC)操作组成。OPs/s(每秒完成操作的数量)指标通过每秒可以完成多少个 MAC(每次乘法和累加各被认为是 1 个 operation,因此 MAC 实际上是 2 个 OP)得到。所以我们可以将利用率定义为实际使用的运算能力和原始运算能力的比值:
\[mac\ utilization = \frac {used\ Ops/s}{raw\ OPs/s} = \frac {FLOPs/time(s)}{Raw\_FLOPs}(Raw\_FLOPs = 1.7T\ at\ 3519)\]二 模型参数量计算
模型参数数量(params):指模型含有多少参数,直接决定模型的大小,也影响推断时对内存的占用量,单位通常为M,GPU端通常参数用float32表示,所以模型大小是参数数量的 4 倍。这里考虑的卷积核长宽是相同的一般情况,都为 K。
卷积层权重参数量 = $ C_i\times K^2\times C_o + C_o$。
$C_i$ 为输入特征图通道数,$K$ 为过滤器(卷积核)尺寸,$C_o$ 为输出的特征图的 channel 数(也是 filter 的数量),算式第二项是偏置项的参数量 。(一般不写偏置项,偏置项对总参数量的数量级的影响可以忽略不记,这里为了准确起见,把偏置项的参数量也考虑进来。)
假设输入层矩阵维度是 96×96×3,第一层卷积层使用尺寸为 5×5、深度为 16 的过滤器(卷积核尺寸为 5×5、卷积核数量为 16),那么这层卷积层的参数个数为 5×5×3×16+16=1216个。
BN 层参数量 = $2\times C_i$。
其中 $C_i$ 为输入的 channel 数(BN层有两个需要学习的参数,平移因子和缩放因子)
全连接层参数量 = $T_i\times T_o + T_O$。
$T_i$ 为输入向量的长度, $T_o$ 为输出向量的长度,公式的第二项为偏置项参数量。(目前全连接层已经逐渐被 Global Average Pooling 层取代了。) 注意,全连接层的权重参数量(内存占用)远远大于卷积层。
2.1 内存访问代价计算
MAC(memory access cost) 内存访问代价也叫内存使用量,指的是输入单个样本(一张图像),模型/卷积层完成一次前向传播所发生的内存交换总量,即模型的空间复杂度,单位是 Byte。
模型参数量的分析是为了了解内存占用情况,内存带宽在某些情况下比 FLOPs 更重要,毕竟在目前的计算机结构下,单次内存访问比单次运算慢得多的多。CNN 网络中每个网络层 MAC 的计算分为:
- 读输入
feature map大小(DDR读)、 - 权重大小(
DDR读)和 - 写输出
feature map大小(DDR写)三部分。
以卷积层为例计算 MAC,可假设某个卷积层输入 feature map 大小是 (Cin, Hin, Win),输出 feature map 大小是 (Hout, Wout, Cout),卷积核是 (Cout, Cin, K, K),理论 MAC(理论 MAC 一般小于 实际 MAC)计算公式如下:
# 端侧推理IN8量化后模型,单位一般为 1 byte
input = Hin x Win x Cin # 输入 feature map 大小
output = Hout x Wout x Cout # 输出 feature map 大小
weights = K x K x Cin x Cout + bias # bias 是卷积层偏置
ddr_read = input + weights
ddr_write = output
MAC = ddr_read + ddr_write
feature map大小一般表示为 (N, C, H, W),MAC指标一般用在端侧模型推理中,端侧模型推理模式一般都是单帧图像进行推理,即N = 1(batch_size = 1),不同于模型训练时的batch_size大小一般大于 1。
三 模型计算量和参数量单位
3.1 浮点计算能力
FLOPS:每秒浮点运算次数,每秒所执行的浮点运算次数,浮点运算包括了所有涉及小数的运算,比整数运算更费时间。下面几个是表示浮点运算能力的单位。我们一般常用 TFLOPS(Tops) 作为衡量 NPU/GPU 性能/算力的指标,比如海思 3519AV100 芯片的算力为 1.7Tops 神经网络运算性能。
MFLOPS(megaFLOPS):等于每秒一佰万(=10^6)次的浮点运算。GFLOPS(gigaFLOPS):等于每秒十亿(=10^9)次的浮点运算。TFLOPS(teraFLOPS):等于每秒万亿(=10^12)次的浮点运算。PFLOPS(petaFLOPS):等于每秒千万亿(=10^15)次的浮点运算。EFLOPS(exaFLOPS):等于每秒百亿亿(=10^18)次的浮点运算。
params : 模型参数量,模型的大小由模型参数量决定。params 通常以单位“百万”(million)或“十亿”(billion)表示,具体地:
M表示百万,是 million 的缩写。因此,当我们说一个模型的参数量为 100M 时,就表示模型有 1 亿个参数,即 100,000,000 个参数。B表示十亿,是 billion 的缩写。当我们说一个模型的参数量为 2B 时,就表示模型有 20 亿个参数,即 2,000,000,000 个参数。
3.2 双精度、单精度和半精度
CPU/GPU 的浮点计算能力得区分不同精度的浮点数,分为双精度 FP64、单精度 FP32 和半精度 FP16。因为采用不同位数的浮点数的表达精度不一样,所以造成的计算误差也不一样,对于需要处理的数字范围大而且需要精确计算的科学计算来说,就要求采用双精度浮点数,而对于常见的多媒体和图形处理计算,32 位的单精度浮点计算已经足够了,对于要求精度更低的机器学习等一些应用来说,半精度 16 位浮点数就可以甚至 8 位浮点数就已经够用了。
对于浮点计算来说, CPU 可以同时支持不同精度的浮点运算,但在 GPU 里针对单精度和双精度就需要各自独立的计算单元。
值得注意的是,模型参数所占用的存储空间取决于参数的数据类型和精度,常见的有:
-
FP64: 双精度浮点数(64位,8 字节)。 FP32: 单精度浮点数(32位,4 字节),包含 1 个符号位、8 个指数位和 23 个⼩数位。FP16: 半精度浮点数(16位,2字节),包含 1 个符号位、5 个指数位和 10 个⼩数位。BF16: IEEE754FP32的截断格式(16位,2字节),包含 1 个符号位,8个指数位,7个小数位。
总结:与 FP32 相比,采用 BF16/FP16 吞吐量(Throughput)基本可以翻倍,内存(RAM)需求可以减半。但是这两者精度上差异不一样,BF16 可表示的整数范围更广泛,它和 float32 的动态范围是等效的,但是尾数精度较小;FP16 表示整数范围较小,但是尾数精度较高。
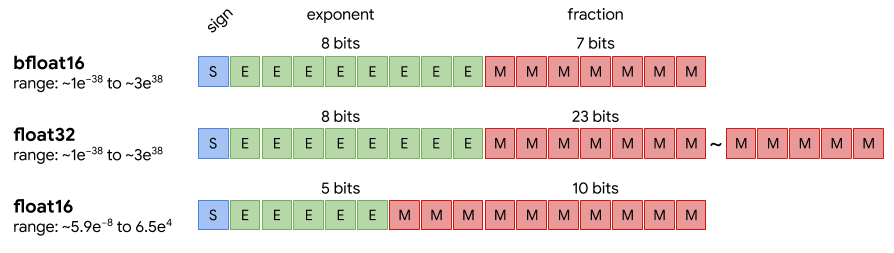
3.3 bfloat16 精度
bfloat16 是谷歌开发的另一种 16 位格式,全称 “Brain Floating Point Format”。最初的 IEEE FP16 格式并不是针对深度学习应用而设计的,其动态范围过窄。BFLOAT16 的提出就是为了解决这个问题,提供了与 FP32 相同的动态范围。
bfloat16 的格式如下所示:
- 符号位:1 bit
- 指数宽度:8bit
- 尾数精度:7bit,而不是经典单精度浮点格式中的 24 位
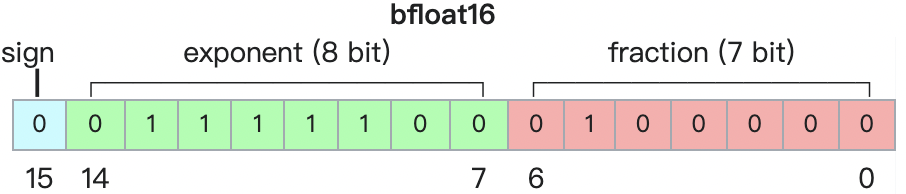
bfloat16 格式其实就是截断的 IEEE 754 FP32,可以和 IEEE 754 FP32 格式快速转换。在转换为 bfloat16 格式时,指数位被保留,而有效数字字段直接通过截断来减少,且忽略 NaN 特殊情况。
神经网络对指数的大小比尾数的大小更灵敏,且与通常需要进行特殊处理(如损失扩缩)的 float16 不同,bfloat16 是在训练和运行深度神经网络时可以直接替代 float32。因此,Google 硬件团队为 Cloud TPU 选择了 bfloat16,用于提高硬件效率,同时保持准确训练深度学习模型的能力,并将 float32 的转换费用降至最低。
3.4 参数量/计算量分析工具
- torchinfo: torchsummay (不再更新)的替代版本,可以一键输出
pytorch模型每层输出feature map大小和参数量、以及模型总的参数量params、计算量MACs等信息,支持多输入模式。 - thop: pytorch-OpCounter: 一键输出模型总的计算量
MACs和参数量params,支持输入自定义算子。
两个工具的安装都很简单,如直接 pip install torchinfo 即可。统计 resnet50 模型的参数量和计算量的示例代码如下所示。
####################卷积神经网络计算量/参数量分析工具#####################
import torchvision, torch
model = torchvision.models.resnet50()
# 1, pytorch 自带输出
# print(model)
# 2, torchinfo 工具
from torchinfo import summary
summary(model, (1, 3, 224, 224), depth=3) # resnet50: 25.557M 4.09G
# 3, thop 工具
from thop import profile, clever_format
input = torch.randn(1, 3, 224, 224)
macs, params = profile(model, inputs=(input, ))
macs, params = clever_format([macs, params], "%.3f")
print("The resnet50 model info: ", macs, params) # resnet50: 4.134G 25.557M
模型输出结果如下所示
==========================================================================================
Layer (type:depth-idx) Output Shape Param #
==========================================================================================
ResNet [1, 1000] --
├─Conv2d: 1-1 [1, 64, 112, 112] 9,408
├─BatchNorm2d: 1-2 [1, 64, 112, 112] 128
├─ReLU: 1-3 [1, 64, 112, 112] --
├─MaxPool2d: 1-4 [1, 64, 56, 56] --
├─Sequential: 1-5 [1, 256, 56, 56] --
│ └─Bottleneck: 2-1 [1, 256, 56, 56] --
│ │ └─Conv2d: 3-1 [1, 64, 56, 56] 4,096
│ │ └─BatchNorm2d: 3-2 [1, 64, 56, 56] 128
│ │ └─ReLU: 3-3 [1, 64, 56, 56] --
│ │ └─Conv2d: 3-4 [1, 64, 56, 56] 36,864
│ │ └─BatchNorm2d: 3-5 [1, 64, 56, 56] 128
│ │ └─ReLU: 3-6 [1, 64, 56, 56] --
│ │ └─Conv2d: 3-7 [1, 256, 56, 56] 16,384
│ │ └─BatchNorm2d: 3-8 [1, 256, 56, 56] 512
│ │ └─Sequential: 3-9 [1, 256, 56, 56] 16,896
│ │ └─ReLU: 3-10 [1, 256, 56, 56] --
│ └─Bottleneck: 2-2 [1, 256, 56, 56] --
│ │ └─Conv2d: 3-11 [1, 64, 56, 56] 16,384
│ │ └─BatchNorm2d: 3-12 [1, 64, 56, 56] 128
│ │ └─ReLU: 3-13 [1, 64, 56, 56] --
│ │ └─Conv2d: 3-14 [1, 64, 56, 56] 36,864
│ │ └─BatchNorm2d: 3-15 [1, 64, 56, 56] 128
│ │ └─ReLU: 3-16 [1, 64, 56, 56] --
│ │ └─Conv2d: 3-17 [1, 256, 56, 56] 16,384
│ │ └─BatchNorm2d: 3-18 [1, 256, 56, 56] 512
│ │ └─ReLU: 3-19 [1, 256, 56, 56] --
│ └─Bottleneck: 2-3 [1, 256, 56, 56] --
│ │ └─Conv2d: 3-20 [1, 64, 56, 56] 16,384
│ │ └─BatchNorm2d: 3-21 [1, 64, 56, 56] 128
│ │ └─ReLU: 3-22 [1, 64, 56, 56] --
│ │ └─Conv2d: 3-23 [1, 64, 56, 56] 36,864
│ │ └─BatchNorm2d: 3-24 [1, 64, 56, 56] 128
│ │ └─ReLU: 3-25 [1, 64, 56, 56] --
│ │ └─Conv2d: 3-26 [1, 256, 56, 56] 16,384
│ │ └─BatchNorm2d: 3-27 [1, 256, 56, 56] 512
│ │ └─ReLU: 3-28 [1, 256, 56, 56] --
├─Sequential: 1-6 [1, 512, 28, 28] --
│ └─Bottleneck: 2-4 [1, 512, 28, 28] --
│ │ └─Conv2d: 3-29 [1, 128, 56, 56] 32,768
│ │ └─BatchNorm2d: 3-30 [1, 128, 56, 56] 256
│ │ └─ReLU: 3-31 [1, 128, 56, 56] --
│ │ └─Conv2d: 3-32 [1, 128, 28, 28] 147,456
│ │ └─BatchNorm2d: 3-33 [1, 128, 28, 28] 256
│ │ └─ReLU: 3-34 [1, 128, 28, 28] --
│ │ └─Conv2d: 3-35 [1, 512, 28, 28] 65,536
│ │ └─BatchNorm2d: 3-36 [1, 512, 28, 28] 1,024
│ │ └─Sequential: 3-37 [1, 512, 28, 28] 132,096
│ │ └─ReLU: 3-38 [1, 512, 28, 28] --
│ └─Bottleneck: 2-5 [1, 512, 28, 28] --
│ │ └─Conv2d: 3-39 [1, 128, 28, 28] 65,536
│ │ └─BatchNorm2d: 3-40 [1, 128, 28, 28] 256
│ │ └─ReLU: 3-41 [1, 128, 28, 28] --
│ │ └─Conv2d: 3-42 [1, 128, 28, 28] 147,456
│ │ └─BatchNorm2d: 3-43 [1, 128, 28, 28] 256
│ │ └─ReLU: 3-44 [1, 128, 28, 28] --
│ │ └─Conv2d: 3-45 [1, 512, 28, 28] 65,536
│ │ └─BatchNorm2d: 3-46 [1, 512, 28, 28] 1,024
│ │ └─ReLU: 3-47 [1, 512, 28, 28] --
│ └─Bottleneck: 2-6 [1, 512, 28, 28] --
│ │ └─Conv2d: 3-48 [1, 128, 28, 28] 65,536
│ │ └─BatchNorm2d: 3-49 [1, 128, 28, 28] 256
│ │ └─ReLU: 3-50 [1, 128, 28, 28] --
│ │ └─Conv2d: 3-51 [1, 128, 28, 28] 147,456
│ │ └─BatchNorm2d: 3-52 [1, 128, 28, 28] 256
│ │ └─ReLU: 3-53 [1, 128, 28, 28] --
│ │ └─Conv2d: 3-54 [1, 512, 28, 28] 65,536
│ │ └─BatchNorm2d: 3-55 [1, 512, 28, 28] 1,024
│ │ └─ReLU: 3-56 [1, 512, 28, 28] --
│ └─Bottleneck: 2-7 [1, 512, 28, 28] --
│ │ └─Conv2d: 3-57 [1, 128, 28, 28] 65,536
│ │ └─BatchNorm2d: 3-58 [1, 128, 28, 28] 256
│ │ └─ReLU: 3-59 [1, 128, 28, 28] --
│ │ └─Conv2d: 3-60 [1, 128, 28, 28] 147,456
│ │ └─BatchNorm2d: 3-61 [1, 128, 28, 28] 256
│ │ └─ReLU: 3-62 [1, 128, 28, 28] --
│ │ └─Conv2d: 3-63 [1, 512, 28, 28] 65,536
│ │ └─BatchNorm2d: 3-64 [1, 512, 28, 28] 1,024
│ │ └─ReLU: 3-65 [1, 512, 28, 28] --
├─Sequential: 1-7 [1, 1024, 14, 14] --
│ └─Bottleneck: 2-8 [1, 1024, 14, 14] --
│ │ └─Conv2d: 3-66 [1, 256, 28, 28] 131,072
│ │ └─BatchNorm2d: 3-67 [1, 256, 28, 28] 512
│ │ └─ReLU: 3-68 [1, 256, 28, 28] --
│ │ └─Conv2d: 3-69 [1, 256, 14, 14] 589,824
│ │ └─BatchNorm2d: 3-70 [1, 256, 14, 14] 512
│ │ └─ReLU: 3-71 [1, 256, 14, 14] --
│ │ └─Conv2d: 3-72 [1, 1024, 14, 14] 262,144
│ │ └─BatchNorm2d: 3-73 [1, 1024, 14, 14] 2,048
│ │ └─Sequential: 3-74 [1, 1024, 14, 14] 526,336
│ │ └─ReLU: 3-75 [1, 1024, 14, 14] --
│ └─Bottleneck: 2-9 [1, 1024, 14, 14] --
│ │ └─Conv2d: 3-76 [1, 256, 14, 14] 262,144
│ │ └─BatchNorm2d: 3-77 [1, 256, 14, 14] 512
│ │ └─ReLU: 3-78 [1, 256, 14, 14] --
│ │ └─Conv2d: 3-79 [1, 256, 14, 14] 589,824
│ │ └─BatchNorm2d: 3-80 [1, 256, 14, 14] 512
│ │ └─ReLU: 3-81 [1, 256, 14, 14] --
│ │ └─Conv2d: 3-82 [1, 1024, 14, 14] 262,144
│ │ └─BatchNorm2d: 3-83 [1, 1024, 14, 14] 2,048
│ │ └─ReLU: 3-84 [1, 1024, 14, 14] --
│ └─Bottleneck: 2-10 [1, 1024, 14, 14] --
│ │ └─Conv2d: 3-85 [1, 256, 14, 14] 262,144
│ │ └─BatchNorm2d: 3-86 [1, 256, 14, 14] 512
│ │ └─ReLU: 3-87 [1, 256, 14, 14] --
│ │ └─Conv2d: 3-88 [1, 256, 14, 14] 589,824
│ │ └─BatchNorm2d: 3-89 [1, 256, 14, 14] 512
│ │ └─ReLU: 3-90 [1, 256, 14, 14] --
│ │ └─Conv2d: 3-91 [1, 1024, 14, 14] 262,144
│ │ └─BatchNorm2d: 3-92 [1, 1024, 14, 14] 2,048
│ │ └─ReLU: 3-93 [1, 1024, 14, 14] --
│ └─Bottleneck: 2-11 [1, 1024, 14, 14] --
│ │ └─Conv2d: 3-94 [1, 256, 14, 14] 262,144
│ │ └─BatchNorm2d: 3-95 [1, 256, 14, 14] 512
│ │ └─ReLU: 3-96 [1, 256, 14, 14] --
│ │ └─Conv2d: 3-97 [1, 256, 14, 14] 589,824
│ │ └─BatchNorm2d: 3-98 [1, 256, 14, 14] 512
│ │ └─ReLU: 3-99 [1, 256, 14, 14] --
│ │ └─Conv2d: 3-100 [1, 1024, 14, 14] 262,144
│ │ └─BatchNorm2d: 3-101 [1, 1024, 14, 14] 2,048
│ │ └─ReLU: 3-102 [1, 1024, 14, 14] --
│ └─Bottleneck: 2-12 [1, 1024, 14, 14] --
│ │ └─Conv2d: 3-103 [1, 256, 14, 14] 262,144
│ │ └─BatchNorm2d: 3-104 [1, 256, 14, 14] 512
│ │ └─ReLU: 3-105 [1, 256, 14, 14] --
│ │ └─Conv2d: 3-106 [1, 256, 14, 14] 589,824
│ │ └─BatchNorm2d: 3-107 [1, 256, 14, 14] 512
│ │ └─ReLU: 3-108 [1, 256, 14, 14] --
│ │ └─Conv2d: 3-109 [1, 1024, 14, 14] 262,144
│ │ └─BatchNorm2d: 3-110 [1, 1024, 14, 14] 2,048
│ │ └─ReLU: 3-111 [1, 1024, 14, 14] --
│ └─Bottleneck: 2-13 [1, 1024, 14, 14] --
│ │ └─Conv2d: 3-112 [1, 256, 14, 14] 262,144
│ │ └─BatchNorm2d: 3-113 [1, 256, 14, 14] 512
│ │ └─ReLU: 3-114 [1, 256, 14, 14] --
│ │ └─Conv2d: 3-115 [1, 256, 14, 14] 589,824
│ │ └─BatchNorm2d: 3-116 [1, 256, 14, 14] 512
│ │ └─ReLU: 3-117 [1, 256, 14, 14] --
│ │ └─Conv2d: 3-118 [1, 1024, 14, 14] 262,144
│ │ └─BatchNorm2d: 3-119 [1, 1024, 14, 14] 2,048
│ │ └─ReLU: 3-120 [1, 1024, 14, 14] --
├─Sequential: 1-8 [1, 2048, 7, 7] --
│ └─Bottleneck: 2-14 [1, 2048, 7, 7] --
│ │ └─Conv2d: 3-121 [1, 512, 14, 14] 524,288
│ │ └─BatchNorm2d: 3-122 [1, 512, 14, 14] 1,024
│ │ └─ReLU: 3-123 [1, 512, 14, 14] --
│ │ └─Conv2d: 3-124 [1, 512, 7, 7] 2,359,296
│ │ └─BatchNorm2d: 3-125 [1, 512, 7, 7] 1,024
│ │ └─ReLU: 3-126 [1, 512, 7, 7] --
│ │ └─Conv2d: 3-127 [1, 2048, 7, 7] 1,048,576
│ │ └─BatchNorm2d: 3-128 [1, 2048, 7, 7] 4,096
│ │ └─Sequential: 3-129 [1, 2048, 7, 7] 2,101,248
│ │ └─ReLU: 3-130 [1, 2048, 7, 7] --
│ └─Bottleneck: 2-15 [1, 2048, 7, 7] --
│ │ └─Conv2d: 3-131 [1, 512, 7, 7] 1,048,576
│ │ └─BatchNorm2d: 3-132 [1, 512, 7, 7] 1,024
│ │ └─ReLU: 3-133 [1, 512, 7, 7] --
│ │ └─Conv2d: 3-134 [1, 512, 7, 7] 2,359,296
│ │ └─BatchNorm2d: 3-135 [1, 512, 7, 7] 1,024
│ │ └─ReLU: 3-136 [1, 512, 7, 7] --
│ │ └─Conv2d: 3-137 [1, 2048, 7, 7] 1,048,576
│ │ └─BatchNorm2d: 3-138 [1, 2048, 7, 7] 4,096
│ │ └─ReLU: 3-139 [1, 2048, 7, 7] --
│ └─Bottleneck: 2-16 [1, 2048, 7, 7] --
│ │ └─Conv2d: 3-140 [1, 512, 7, 7] 1,048,576
│ │ └─BatchNorm2d: 3-141 [1, 512, 7, 7] 1,024
│ │ └─ReLU: 3-142 [1, 512, 7, 7] --
│ │ └─Conv2d: 3-143 [1, 512, 7, 7] 2,359,296
│ │ └─BatchNorm2d: 3-144 [1, 512, 7, 7] 1,024
│ │ └─ReLU: 3-145 [1, 512, 7, 7] --
│ │ └─Conv2d: 3-146 [1, 2048, 7, 7] 1,048,576
│ │ └─BatchNorm2d: 3-147 [1, 2048, 7, 7] 4,096
│ │ └─ReLU: 3-148 [1, 2048, 7, 7] --
├─AdaptiveAvgPool2d: 1-9 [1, 2048, 1, 1] --
├─Linear: 1-10 [1, 1000] 2,049,000
==========================================================================================
Total params: 25,557,032
Trainable params: 25,557,032
Non-trainable params: 0
Total mult-adds (G): 4.09
==========================================================================================
Input size (MB): 0.60
Forward/backward pass size (MB): 177.83
Params size (MB): 102.23
Estimated Total Size (MB): 280.66
==========================================================================================
[INFO] Register count_convNd() for <class 'torch.nn.modules.conv.Conv2d'>.
[INFO] Register count_normalization() for <class 'torch.nn.modules.batchnorm.BatchNorm2d'>.
[INFO] Register zero_ops() for <class 'torch.nn.modules.activation.ReLU'>.
[INFO] Register zero_ops() for <class 'torch.nn.modules.pooling.MaxPool2d'>.
[INFO] Register zero_ops() for <class 'torch.nn.modules.container.Sequential'>.
[INFO] Register count_adap_avgpool() for <class 'torch.nn.modules.pooling.AdaptiveAvgPool2d'>.
[INFO] Register count_linear() for <class 'torch.nn.modules.linear.Linear'>.
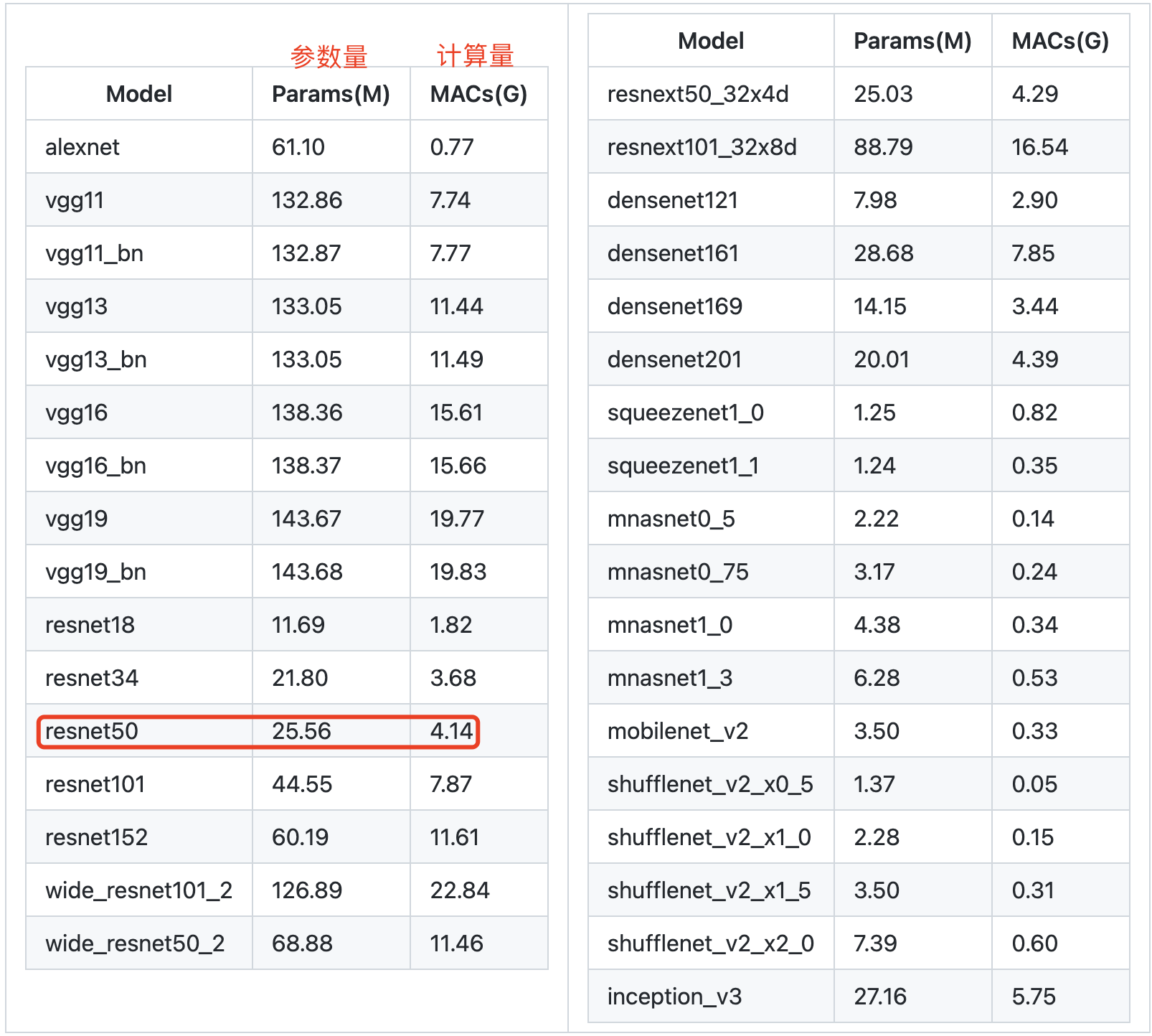
值得注意的是,不同工具统计出来的模型计算量和参数量可能不一样,因为计算方式不一样,但是都是比较准确的。使用 thop 工具统计的经典 backbone 的 Params 参数量与 FLOPs 计算量如下表所示: