深入理解 roofline 模型

Categories: Hpc

一 Roofline 性能分析模型

1.1 Roofline 模型原理

为了做性能分析，Roofline 模型论文引入了“操作强度”（operational intensity）这个概念，表示每字节 DRAM 数据传输（traffic）所对应的操作次数（每字节 flops），这里的字节数是指那些经过缓存层过滤后进入主内存 DRAM 的字节，即我们关注的是缓存与内存之间的数据传输，而不是处理器与缓存之间的数据传输（traffic）。因此，操作强度可以用来评估特定计算机上某个内核所需的 DRAM/HBM 带宽。

操作强度公式定义如下：

\[\text{OI} = \frac{\text{总浮点操作数（FLOPs）}}{\text{总内存访问量（Bytes）}}\]

Roofline 模型可视化曲线如下图所示：

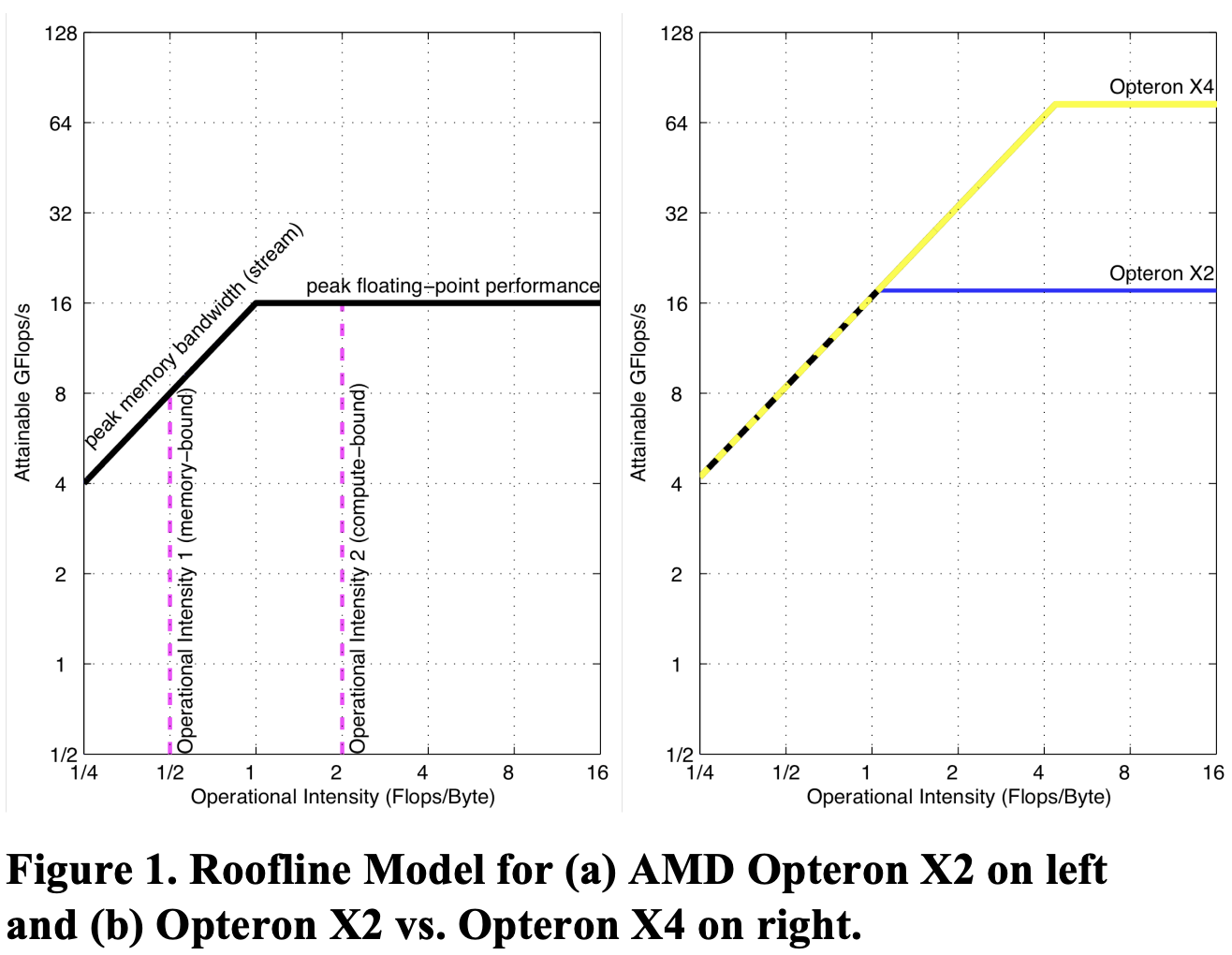
Roofline Model for (a) AMD Opteron X2 on left and (b) Opteron X2 vs. Opteron X4 on right.

Roofline 模型曲线图的 X 轴表示 Flops/byte（GFlops per byte）即操作强度，Y 轴表示 GFlops/s（GFlops per second）。

  • 通过绘制一条水平线表示计算机的峰值浮点性能，任何浮点运算的实际性能都不会超越这条线，因为它代表硬件限制。
  • 通过绘制一条斜线，表示该计算机内存系统在不同操作强度下支持的最大浮点操作性能。公式如下：\(\text{可实现的 GFlops/sec} = \text{Min(峰值浮点操作性能，峰值内存带宽 x 操作强度)}\)
  • 斜线和直线的交点对应的是处理器同时达到峰值浮点操作性能和峰值内存带宽的条件，这发生在特定的操作强度下。\(\text{芯片的操作强度 = 峰值浮点操作性能/峰值内存带宽}\)
\[\text{Attainable GFlops/sec} = \text{Min(Peak Floating Point Performance, Peak Memory Bandwidth} \times \text{Operational Intensity)}\]

水平和斜线的组合为该模型命名为“Roofline model”。Roofline 模型为每个内核算法设定了性能上限，具体取决于内核的操作强度。形象理解的话，我们可以将操作强度视为触及屋顶的一个柱子。

  • 如果触及平坦的屋顶部分，表明性能受计算限制；
  • 如果触及斜屋顶部分，表明性能受内存限制。

在图 1a 中，操作强度为 2 的内核受芯片计算限制，而操作强度为 1 的内核受芯片内存限制。可以在不同内核上重复使用 Roofline model，而芯片的 Roofline 模型曲线不会变化。

1.2 Roofline 模型数学表达

如果需要用数学公式表示 Naive Roofline 模型，可以表示为如下：

\[P_{max} = min(P_{peak}, I*b_{max})\]

$P_{max}$: 浮点操作性能上限 [操作数/秒]

CPU/NPU/GPU 芯片相关参数：

  • $P_{peak}$: 可用的峰值浮点性能 [操作数/秒]
  • $b_{max}$: 可用的峰值内存带宽 [字节/秒]

内核/算子相关参数：

  • $I$: 计算强度 [操作数/字节] $ = \frac{\text{总浮点操作数（FLOPs）}}{\text{总内存访问量（Bytes）}}$

1.3 Roofline 模型作用

Roofline 性能分析模型通过将算法 kernel 的实际操作强度和芯片硬件的理论最大操作强度对比，以揭示 kernel 是受到计算性能的限制还是受到内存带宽的限制。性能瓶颈分析过程：

  • 内存受限：当算子/模型的算术强度 < (CPU/GPU)芯片的 OI，性能受内存带宽限制，需要想办法减少算子的内存交换次数 MAC。
  • 计算受限：当算子/模型的算术强度 > (CPU/GPU)芯片的 OI，受限于处理器的计算性能，需要想办法减少算子的浮点运算次数 FLOPs

总结：Roofline 可以帮助识别程序/内核的性能瓶颈，并指导优化（减少内存访问次数还是算法计算量 FLOPs），以及是否达到了硬件的能力上限。

下表是 v100、a100、h100 卡的常用性能指标和 FP16 Tensor 算力的操作强度 oi:

GPU 显存 CUDA 核心数 FP16 Tensor Core 浮点运算能力 FP32 浮点运算能力 最大内存带宽 Tensor 运算强度（OI）
V100-SXM 16 GB 5120 125 TFLOPS 15.7 TFLOPS 900 GB/s 138 TOPS (FP16)
A100-SXM 40 GB / 80 GB 6912 312 TFLOPS 19.5 TFLOPS 2039 GB/s 153 TOPS (FP16)
H100-SXM 80 GB 8192 989 TFLOPS(不开启稀疏计算) 60 TFLOPS 3350 GB/s 295 TOPS (FP16)

V100 PCle GPU 的峰值算力为 112 FP16 Tensor TFLOPS，片外内存带宽约为 900 GB/s，芯片上 L2 缓存的带宽为 3.1 TB/s，因此其 ops:byte ratio 在 40 到 124.4 = 112 / 0.9 之间，取决于操作数据的来源（片内或片外存储器）。

在深度学习模型推理中，SRAM（片内存储器）是存不下全部模型权重的， 在 A100 GPU 中，ops:byte ratio 是 208，这意味着：

  • 每访问 1 字节内存时，GPU 可以完成 208 次浮点运算。
  • 如果我们计算的 OI（FLOPs/byte）低于 208，程序性能会受到内存带宽的限制。

二 Roofline 性能分析示例

2.1 计算 kernel 的 Roofline 性能分析

矩阵乘法: $A\times B = C$，其中 $A\in \mathbb{R}^{M\times k}, B \in \mathbb{R}^{M\times N},C \in \mathbb{R}^{M\times N}$，数据类型为 FP16，它的 Roofline 性能瓶颈分析如下：

\[\text{OI}_\text{matmul} = \frac{2MNK}{MK + KN +MN} \\ \text{ops/bytes}_\text{A100} = \frac{312}{2.03} = 153\]

在 A100_SXM 卡上运行，如果 $\text{OI}_\text{matmul} < 153$，则矩阵乘法处于内存受限，反之则计算受限。

在 V100_PCIE 卡上运行，假设在 FP16 输入上进行 Tensor Core 操作，并使用 FP32 累积，下表显示了一些常见网络层的算术强度。

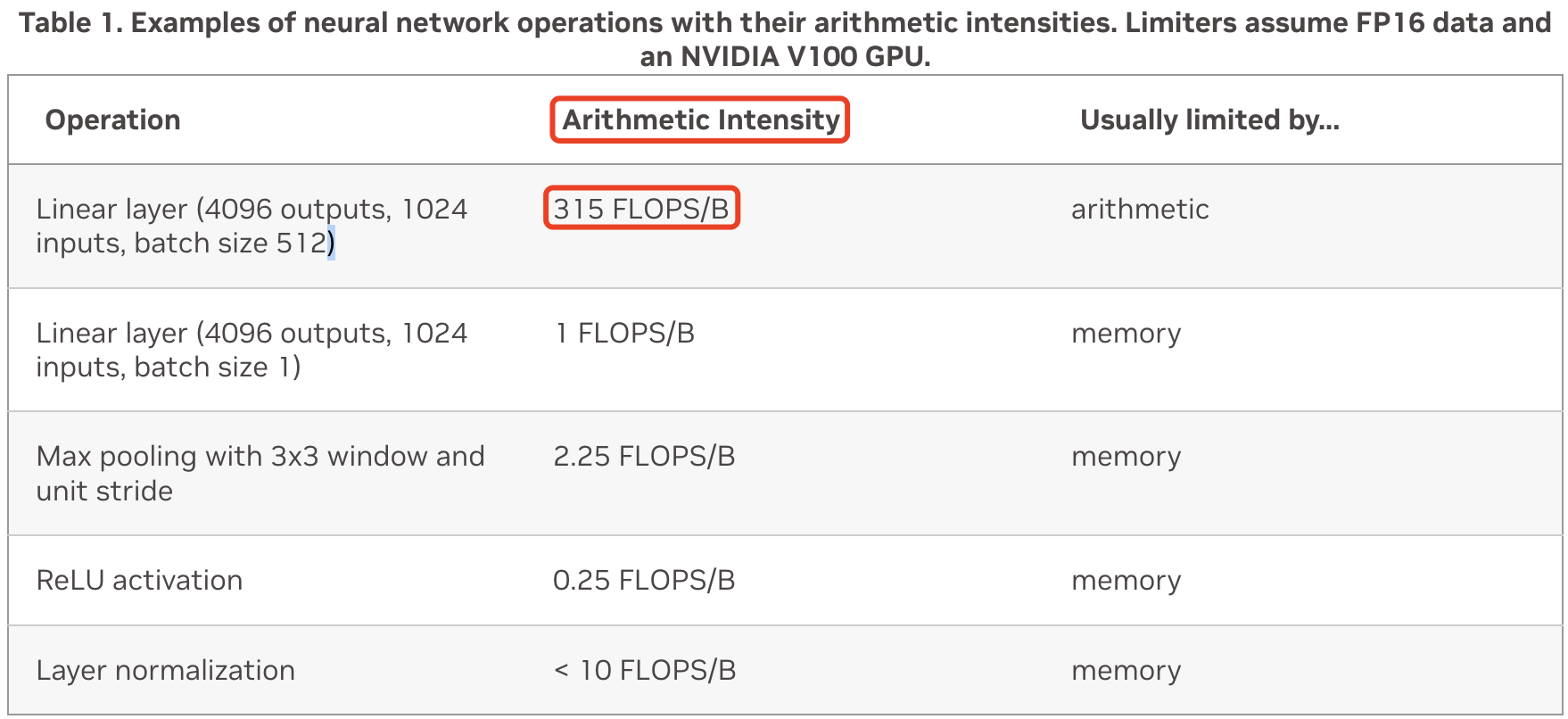
memory_math_bound

上述表格第一行的计算过程如下:

\[\begin{aligned} \text{arithmetic intensity} &= \frac{\text{FLOPs}}{\text{MAC}} = \frac{\#op}{\#bytes}\\ &= \frac{2MKN}{2(MK + KN + MN)} \\ &= \frac{2 \cdot 512 \cdot 1024 \cdot 4096}{2 \cdot (512\cdot1024 + 1024\cdot4096 + 512\cdot 4096 )} \\ &\approx 315 \end{aligned}\]

即该线性层（矩阵乘法）的算术强度为 $315$，大于 V100 PCle 的 $124.4$。因此，在 V100 PCle 上，该矩阵乘法受到算术限制，即 GPU 将被充分利用。

2.2 LLM 推理的 Roofline 性能分析

对于 A100 卡，其 GPU 的HBM 内存带宽为 2039 GB/s，GPU 的理论 FP16 计算能力为 312 TFLOPs（$312 * 10^{12}$FLOPs），因此芯片 Tensor 运算强度 $OI = 312 * 10^{12} / 2039 * 10^{9} = 153$

实际 llm 推理的内存占用和传输数据量的分析是非常复杂且要考虑不同应用场景、不同推理框架、不同优化模式等等，因此为了简化分析过程，这里考虑的是理想情况下的分析，且是非超长上下文场景聊天情形：conext_lenght < 1024，提示词的长度较小时其值 « hidden_size，这个时候 llm 的参数、计算量分析都可以更为简单，且有类似结论：“在一次前向传播中，对于每个 token 和 每个模型参数，需要进行 2 次浮点数运算”，分析过程见这篇文章。

考虑理想场景且 batch_size = 1，很明显，随着输入提示词长度的增加，llm 的操作强度成线性增加！

  • prefill 阶段：当 seq_len > 200 时，llm 操作强度达到了 $400 = \frac{\text{flops}}{\text{memory acces}} = 2*200$，很明显 llm 在 prefill 阶段基本都是是计算受限的。
  • decode 阶段：seq_len 固定且 = 1，llm 推理时的操作强度也固定为 $2 = \frac{\text{flops}}{\text{memory acces}}$，很明显 llm 在 decode 阶段基本都是是内存受限的。

总结：llm 推理时，prefill 和 decode 阶段是处于不同瓶颈的，那么其执行过程是否可以完全分开呢？包括但不限于计算/数据存储在不同的节点机器上。

三 AI 应用性能优化策略

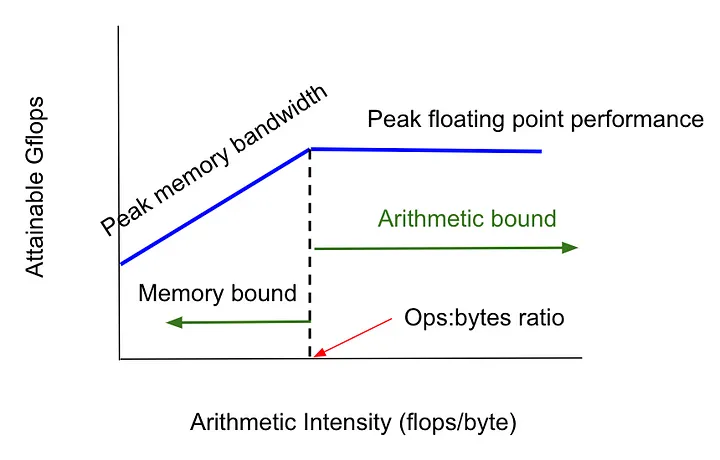
roofline model picture
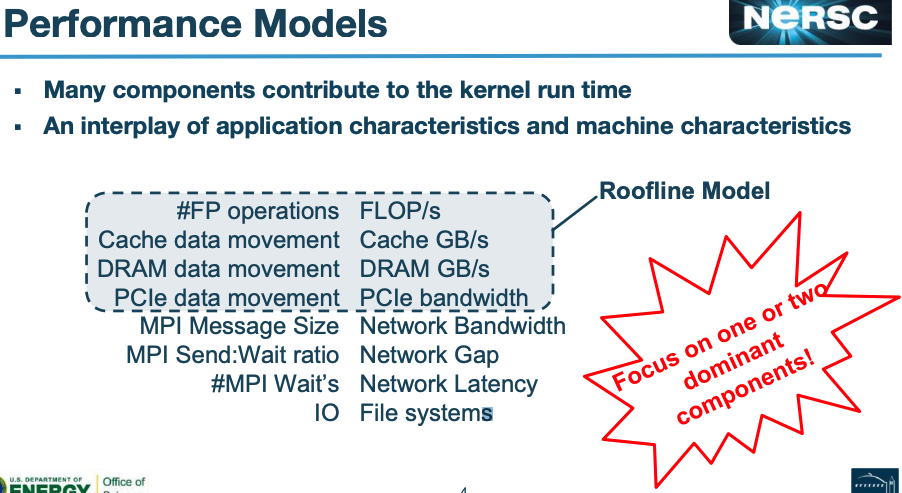
Many components contribute to the kernel run time
roofline_time

总结：

  1. AI 应用的推理时间取决于多个因素，我们应该关注主要因素，比如：内存读写和数学计算时间，而不是次要因素：网络带宽和磁盘读写时间。
  2. Roofline Model 有两个区域：内存带宽受限和算力受限区域，分别对应两种不同的优化策略：硬件不变的前提下，优化模型结构/内核算法，目的是减少内存访问代价 MAC 或者浮点运算次数 FLOPs。
  3. AI 模型推理的实际时间取决于内存读取时间和 CPU/GPU 数学（乘加）计算时间，取决于哪个时间更长。一般来讲，当处于内存受限时，内存读取时间长；当处于算力受限时，数学计算时间长。

以 A100 GPU 为例，该硬件的 ops:byte ratio 是 $208$（V100 是 $138.9$），假设在 llm 推理中，计算一个 token 的 kv 值的计算强度是 1，那么计算 208 个 tokens 的 kv 值的计算强度则是 208（kv 计算量和 seq_len 线性相关）。

这也意味着如果我们计算一个 token 的 kv 值，与计算多达 208 个 token 的时间几乎是相同的！因为低于这个数，会受到内存带宽的限制，且内存加载时间 > 数学计算时间；高于这个数，我们会受到算力 FLOPS 的限制。

这也可以延伸出，当 llm 推理时的操作强度低于硬件的 ops:byte ratio（如 208），则内存加载时间主导性能。

前面的假设中，为什么计算 1 个 token 和 208 个 token 的时间几乎相同？

  • 当只计算 1 个 token 时，操作强度非常低，程序性能主要受限于内存读取时间，而数学计算时间占比很小，即程序性能是由内存带宽指导。
  • 计算 1 个 token 时，GPU 需要加载相关的权重数据到缓存中。计算 208 个 token 时，GPU 也是使用同样的权重数据。
  • 因为权重加载的时间是固定的，计算更多 token 并不会显著增加内存传输时间。

参考资料

你觉得有收获吗？❤️
Read More

Roofline 论文解读

【2024-09-14】翻译 roofline 性能分析模型论文。