llm 参数量-计算量-显存占用分析
Categories: Transformer
背景知识
感谢群友-每天汲取一点点指出的公式书写错误、计算量排版和最大并发量估计公式建议。
chatgpt 的火热引爆了 llm(大语言模型) 的研究和发展,llm 的大体现在两个方面:模型参数和训练数据规模,这进而带来了两个挑战:gpu 内存访问和计算效率。
目前的 llm 都是基于 transformer 模型,得益于 GPT 模型的成功,主流的模型架构是采用 decoder-only 架构的,同时模型的输出是自回归的形式,所以 gpt 这类模型也叫做 Causal LM。
因果建模模型、自回归模型、生成式 generative 模型所代表的意义几乎一致。
本文分析的是采用 decoder-only 框架的 llm(类 gpt 的大语言模型)的参数量 params、计算量 FLOPs、理论所需 CPU 内存和 GPU 显存。
这里简单介绍下 decoder-only 架构的 llm 结构,其只采用 Transformer 模型中的解码器(Decoder)部分,同时 decoder 结构去掉了 Encoder-Decoder attention(Decoder 中的第二个 attention),只保留了 Masked Self-Attention。这里以 gpt1 模型为例,其模型结构如下所示:
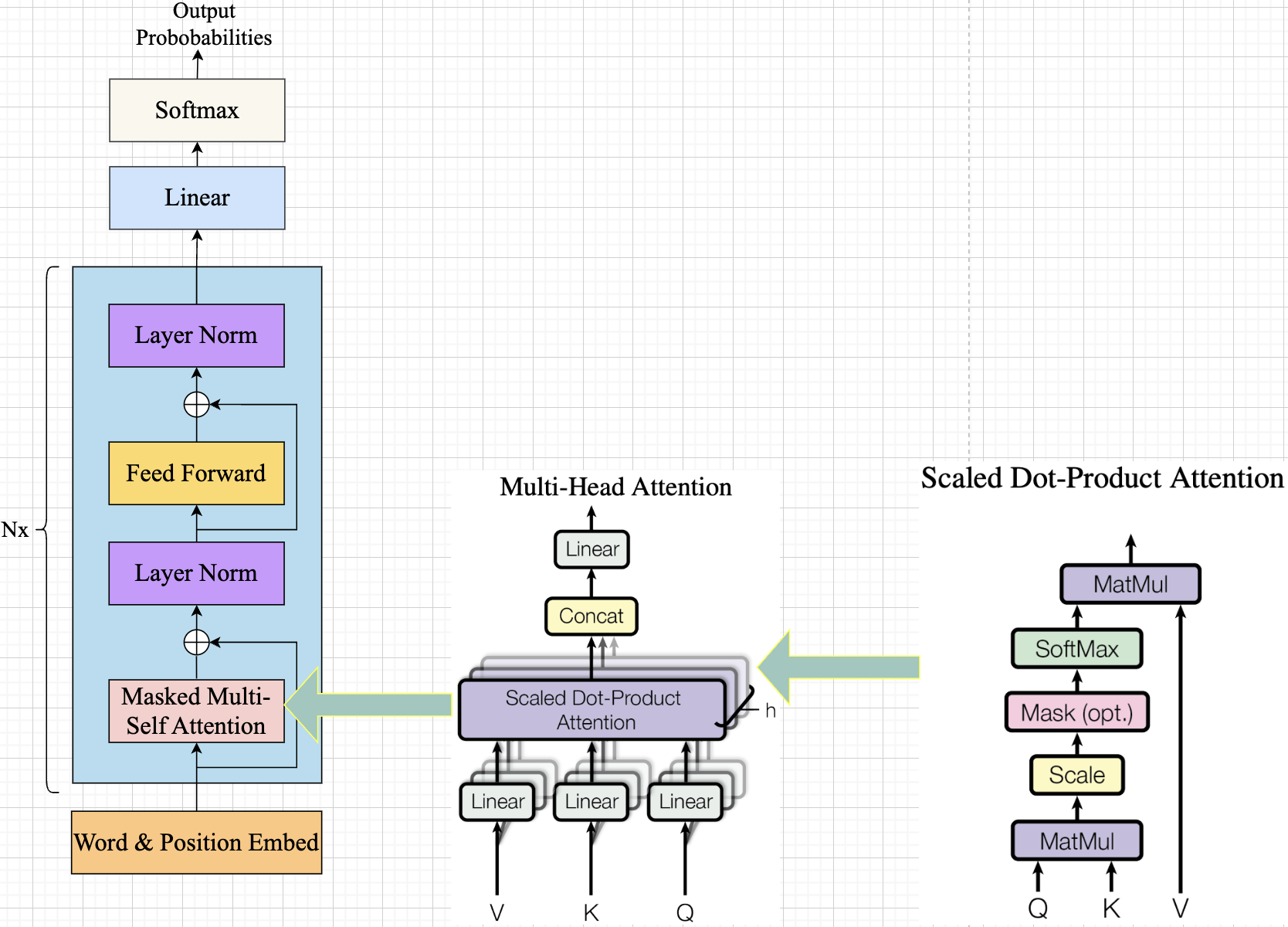
gpt 模型结构,llama 在细节上会有所区别,但是主要网络层不会变。
[(masked)multi_headed_attention --> layer_normalization --> MLP -->layer_normalization]* N -> Linear -> softmax -> output probs
与正常的 Attention 允许一个位置关注/看见到它两边的 tokens 不同,Masked Attention 只让模型看到左边的 tokens:
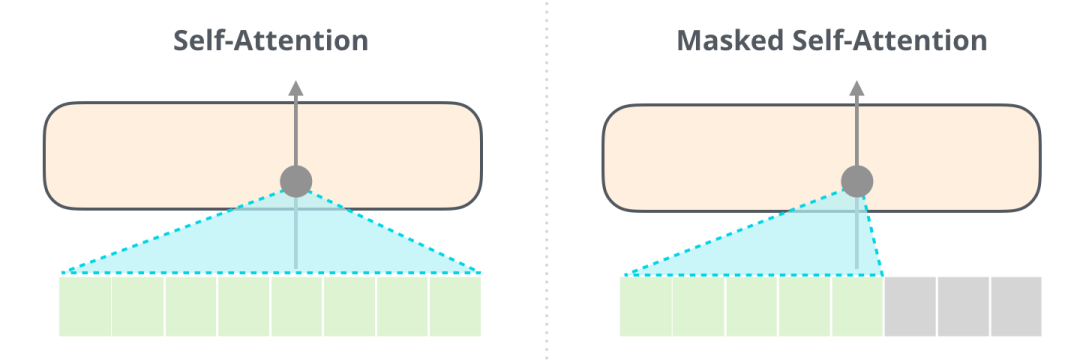
图: self attention vs mask self attention
在计算模型参数量/计算量之前,我们先定义好一些表示符号:
- $b$: 批量大小
batch_size。 - $s$: 输入序列长度
seq_len,即输入prompt字符串的长度。 - $o$: 输出
tokens数量,用于计算 kv cache 的形状。 - $h$: 隐藏层的维度,也叫 $d_{model}$,即序列中每个
token的embedding向量的维度。它定义了输入和输出的特征向量的大小,也是模型内部各个组件(特别是注意力机制和前馈网络)操作的主要向量维度。 - $V$:词表大小
vocab_size。也是每个 token 在做 embedding 前的 one-hot 向量维度。 - $n$:模型中 decoder layers 层数,对应 hf 模型配置文件中的 num_hidden_layers。
这些变量值都可以在模型配置文件中找到,以 llama-13b 模型配置文件为例,主要字段解释如下:
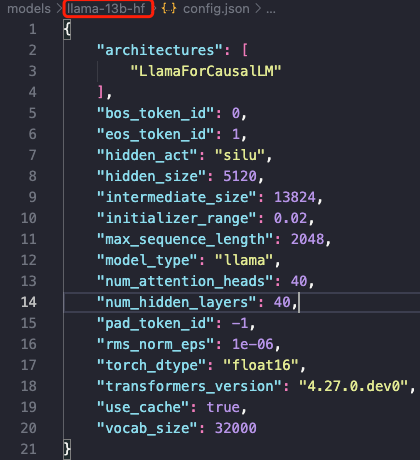
vocab_size:词汇表中标记的数量,也是嵌入矩阵的第一个维度。hidden_size:模型的隐藏层大小,其实就是 $d_\text{model}$。num_attention_heads:模型的多头注意力层中使用的注意力头数量。num_hidden_layers:模型中的块数(层数), number of layers。max_sequence_length: $2048$, 即代表预训练的 LLaMA 模型的最大 Context Window 只有 $2048$,也是模型支持的最大输入上下文长度。
后续的 llama2-3/qwen2 模型都用 max_position_embeddings 参数表示模型支持的最大输入上下文长度,比如qwen2.5-3b 模型支持的最大上下文长度为 32768(32k)。
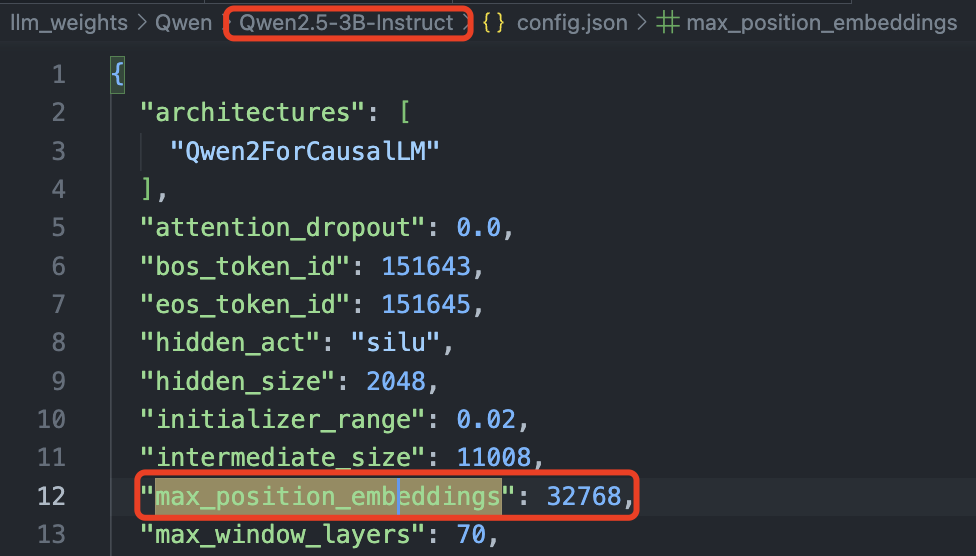
注意,很多 decoder-only 架构的自回归模型的全连接层的偏置 bias 都设置为 False,故这里的计算公式中没有考虑偏置参数。
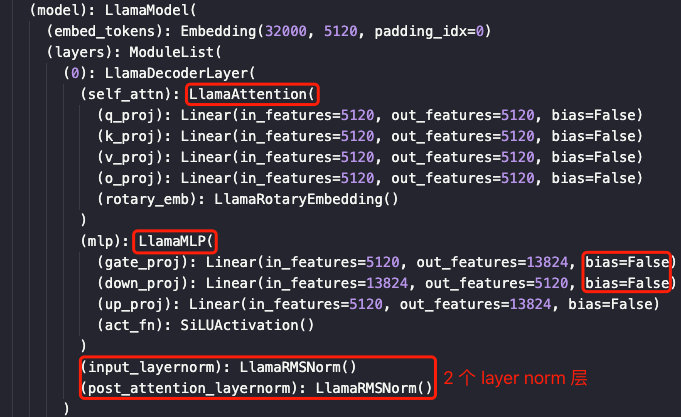
一 模型参数量
模型由 $N$ 个相同的 decoder block 串联而成,每个 decoder block 又由 1 个带掩码(mask)多头注意力(MHA)层、1 个前馈神经网络(MLP)层和 2 个层归一化层组成。
这里不单独计算每个 self-attention 层的参数量了,毕竟实际代码中,其都是在一个矩阵中。另外
llama模型的MLP块虽然有 3 个线性层,但其参数量和计算量和gpt1是一样的。
1,MHA 块有 $4$ 个线性层(全连接层/映射层),对应的是 $Q$、$K$、$V$ 和输出映射层的权重矩阵 $W_Q,W_K,W_V,W_o \in \mathbb{R}^{h\times h}$ 及其偏置。$4$ 个线性层权重参数形状都为 $[h,h]$,偏置形状为 $[h]$。MHA 块的参数量 = $4h^2 + 4h$
2,MLP/FFN 块由 $2$ 个线性层组成,一般第一个线性层完成 $h$ 到 $4h$ 的升维,第二个将 $4h$ 降维到 $h$。对应权重矩阵为 $W_1\in \mathbb{R}^{h\times 4h}$, $W_2 \in \mathbb{R}^{4h\times h}$,偏置形状分别为 $4h$ 和 $h$。MLP 块的参数量 = $8h^2 + 5h$。
3,LN 层有两个,分别连接在 MHA 和 MLP 块的后面,layer norm 层有两个可训练参数: $\mu_{\beta}$ 和 $\sigma_{\beta}$(scale factor and offset),参数大小都是 $[h]$。$2$ 个 Layer Norm 层的总参数量 = $4h$。
4,除了 decoder block 有很多参数,Embedding 层同样也有参数,Embedding 层包括两部分: Token Embedding (TE) 和 Positional Embedding (PE)。TE 层的输入张量形状是 $[b, s, V]$,输出维度是 $[b, s, h]$,对应的 TE 层权重矩阵形状为 $[V, h]$,即 TE 层参数量 = $Vh$。另外,最后的输出层通常是和 TE 层共享权重矩阵的。
位置 Embedding 层一般使用纯数学计算,无需经过训练,故忽略不计。
综上可知,参数量和输入序列长度无关。对于有 $n$ 层 decode block 块的 llm 参数量为 $n(12h^2 + 13h) + Vh$。当 $h$ 较大时,可忽略一次项,llm 参数量近似为 $12nh^2$。
不同版本 LLaMA 模型的参数量估算如下:
| 实际参数量 | 隐藏维度 h | 层数 n | heads 数目 | 预估参数量 12nh^2 |
|---|---|---|---|---|
| 6.7B | 4096 | 32 | 32 | 6,442,450,944 |
| 13.0B | 5120 | 40 | 40 | 12,582,912,000 |
| 32.5B | 6656 | 60 | 52 | 31,897,681,920 |
| 65.2B | 8192 | 80 | 64 | 64,424,509,440 |
另外,推特上有人研究了 gpt-like 模型(opt)的参数分布,下面是不同大小模型的一些图。可以看出,随着模型变大,MLP 和 Attention 层参数量占比越来越大,最后分别接近 2/3 和 1/3。这个比例可以通过上面的公式推测出来,估算公式:
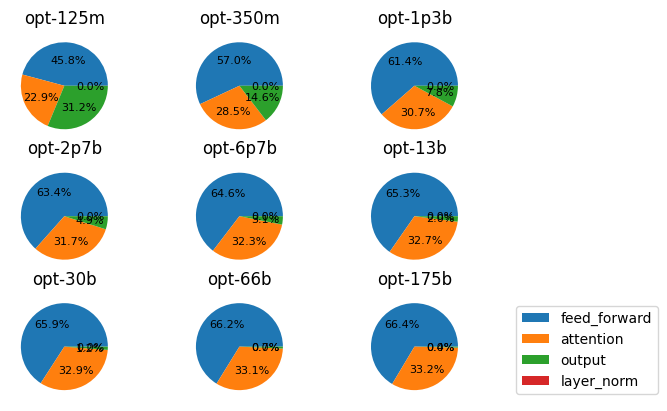
1.1 CPU 内存使用量
1,模型参数内存如何计算?
- 对
int8而言,模型参数内存 = 参数量 *(1字节/参数),单位字节数 - 对
fp16和bf16而言,模型参数内存 = 参数量 *(2 字节/参数)
llm 模型一般都是保存为 fp16 或者 bf16 格式,以 llama13b 为例,$1\text{B} = 10^9 \text{byte} \simeq 1\text{GB}$,可知 llam13b 模型权重参数文件占用的存储空间是 26GB 左右。
2,模型推理需要的总 cpu 内存是多少?
推理总内存 ≈ 1.2 × 模型参数内存(20% 是经验,不同框架可能不一样)
二 计算量分析
FLOPs:floating point operations 指的是浮点运算次数,一般特指乘加运算次数,理解为计算量,可以用来衡量算法/模型时间的复杂度。
对于矩阵 $A\in\mathbb{R}^{1\times n}$ 和 $B \in \mathbb{R}^{n\times 1}$ 的矩阵乘法的 FLOPs 为 $2n$;对于矩阵 $A \in \mathbb{R}^{m\times n}$ 和 $B\in\mathbb{R}^{n\times p}$ 的矩阵乘法的 FLOPs 为 $2mnp$。
Pytorch 实现线性层的函数为 nn.Linear(in_features, out_features, bias=True),其中线性层权重的的维度大小是 $[下一层的维数/out_{features},前一层的维数/in_{features}]$,对应的计算公式为:
线性层(全连接层/映射层)的 FLOPs 计算:假设 $I$ 是输入层的维度,$O$ 是输出层的维度,对应全连接层(线性层)的权重参数矩阵维度为 $[I, O]$。
- 不考虑 bias,全连接层的 $FLOPs = (I + I -1) \times O = (2I − 1)O$
- 考虑 bias,全连接层的 $FLOPs = (I + I -1) \times O + O = (2\times I)\times O$
对于 transformer 模型来说,其计算量主要来自 MHA 层和 MLP 层中的矩阵乘法运算。先考虑 batch_size = 1 和 输入序列长度为 $s$ 的情况。
2.1 MHA(Attention) 层计算量
对于 Attention 层,输入输出矩阵 QKVO 大小一模一样,形状都是 $[s,h]$。
2.1.1 prefill 阶段
先分析 MHA 块的计算量:
1, 计算 Q、K、V:对输入矩阵做线性变换,输入 tokens 序列的 embedding 向量的形状为 $[s, h]$,做线性变换的权重矩阵 $W_Q$、$W_K$、$W_V$ $\in \mathbb{R}^{h\times h}$,矩阵乘法的输入输出形状为: $[s,h] \times [h,h]\to [s,h]$,FLOPs: $3* 2sh^2 = 6sh^2$。
2, Self-Attention 层,MHA 包含 heads 数目的 Self-Attention 层,这里直接分析所有 Self-Attention 层的 FLOPs:
- $QK^T$ 打分计算:每个头需要计算 Query 和 Key 的点积,所有头的 $QK^T$ 矩阵乘法的输入和输出形状为: $[s,h] \times [h,s]\to [s,s]$,
FLOPs: $2s^2h$。 - softmax 函数:softmax 函数不会改变输入矩阵的维度,即 $[s,s] \to [s,s]$,native softmax 涉及
FLOPs$(4/5)sh$。 - 应用注意力权重:计算在 $V$ 上的加权 $score\cdot V$,矩阵乘法的输入输出形状: $[s,s] \times [s,h]\to [s,h]$,
FLOPs: $2s^2h$。
attention_scale($/\sqrt(k)$)是逐元素操作、attn_softmax ($\text{softmax}$) 的计算量较小,因此都忽略不计。故Scale Dot Product Attention 层内部只估算两个矩阵乘法的计算量为 $4s^2h$。
3, 多头拼接和线性映射:所有注意力头输出拼接后通过线性映射,concat 不涉及数学运算,只涉及内存操作。矩阵乘法的输入和输出形状为: $[s,h] \times [h,h]\to [s,h]$,attention 后的线性映射的 FLOPs: $2sh^2$。
综上,prefill 阶段 MHA 块的 FLOPs: $6sh^2 + 4s^2h + 2sh^2 = 8sh^2 + 4s^2h$
2.1.2 decode 阶段
1,计算 Q、K、V:每个 token 的 embedding 向量 $t_e \in \mathbb{R}^{1\times h}$,对应的,3 个矩阵乘法的输入和输出形状为: $[1,h] \times [h,h]\to [1,h]$,FLOPs: $3*2h^2 = 6h^2$。
2,Self-Attention 层:
- $QK^T$:矩阵乘法的输入输出形状为: $[1, h] \times [h, s+o]\to [1,s+o]$,
FLOPs: $2h(s+o)$。 - $\text{score}\cdot V$: 矩阵乘法的输入输出形状为: $[1, s+o] \times [s+o, h]\to [1, h]$,
FLOPs: $2h(s+o)$。
通过上述两个公式,可以看出随着输出 token 的增加,计算量也随之线性增加,这也是我们在 llm 推理时观察到的越到后生成 token 越慢的原因。
在实际代码中,对于每一轮解码的 flops 上述公式有时等效于: $2sh$?
3,输出线性映射层: 矩阵乘法 matmul 的输入输出形状为: $[1, h] \times [h, h]\to [1, h]$,FLOPs: $2h^2$。
综上,decode 阶段 MHA 层每一轮解码的 FLOPs: $6h^2 + 4(s+o)h + 2h^2= 8h^2 + 4(s+o)h$。
2.1.3 kv cache 节省了多少计算量
这里,我简单分析,对于上下文长度 $s$,不使用 kv cache d的 self-attention 的总计算量复杂度为:总计算量:$O(s^3h)$,使用后的总计算量近似为 $Os^2h$。计算量节省比率:
\[\text{节省比率} = \frac{O(s^3 h) - O(s^2 h)}{O(s^3 h)} = 1 - \frac{1}{s}\]当 $s$ 较大时,$\frac{1}{s}$ 接近于 0,节省比率接近于 100%!
换种说法,计算复杂度从 $O(s^3 h)$ 降低到 $O(s^2 h)$,即使用 kv cache 可节省约 $s$ 倍的计算量,输出 tokens 数越多,计算量节省越可观。
2.2 MLP 层计算量
prefill 阶段
先分析 prefill 阶段 Feed-forward(MLP/FFN)层的计算量分析。包含两个线性层,以及一个 relu 激活层(逐元素操作,flops 很小$=5\cdot 4h$,可忽略)。MLP 两个线性层的权重参数矩阵: $W_1 \in \mathbb{R}^{h\times 4h}$、$W_2 \in \mathbb{R}^{4h\times h}$,MLP 的输入矩阵: $\in \mathbb{R}^{s\times h}$。
- 第一个线性层,线性层对应矩阵乘法的输入和输出形状为 $[s,h] \times [h,4h]\to[s,4h]$,
FLOPs为 $8sh^2$ - 第二个线性层,矩阵乘法的输入和输出形状为 矩阵乘法的输入和输出形状为 $[s,4h] \times [4h, h]\to [s,h]$,
FLOPs为 $8sh^2$
因此,prefill 阶段 MLP 层的 FLOPs: $2*8sh^2 = 16sh^2$。
decode 阶段
除了 MHA 层的 FLOPs 计算公式需要明显区分 prefill 和 decode 阶段,其他层只需要将 prefill 阶段的计算公式中的 $s$ 设置为 $1$。即对于 decode 阶段的 MLP 层的 FLOPs = 16h^2
2.3 模型总计算量
除了 MHA、MLP 块的计算量之外:
Embedding层只是一个查找表,没有进行显式的乘法运算,因此严格来说,Embedding 层本身不会产生FLOPs,但可以通过其输出维度来推导其他层的FLOPs。LayerNorm操作是逐元素进行的,因此不存在通用的公式来。LayerNorm层的两个权重都是一个长度为 $h$ 的向量,FLOPs可以预估为: $2h$,但通常忽略不计。- 最后的输出层(线性层)的将隐藏向量映射为词表大小,得到每个 token 对应的 logits 向量。线性层的权重矩阵为:$W_{last} \in \mathbb{R}^{h\times V}$,矩阵乘法的输入和输出形状为: $[s, h] \times [h, V] -> [s, V]$。
FLOPs: $2shV$。
综上分析可知,$n$ 层 decoder block/layer 的总计算量大约为: $n(8sh^2 + 4s^2h + 16sh^2) = 24nh^2s + 4nhs^2$。而在输入数据形状为 $[b, s]$ 的情况下,一次训练/推理:
1,prefill 阶段总的计算量:
2,decode 阶段每轮的计算量:
\(b\times (8nh^2 + 4nh(s+o) + 16nh^2) + 2bhV = 2 4nh^2*b + 4nhb(s+o) + 2bshV\)
关于 llm flops 的估算,其实还有一个很简单的方法,就是直接估算每个 token 的 flops 且只分析 qkv和输出层的矩阵计算,以及 mlp 层的矩阵计算,这种分析过程更简单,可以直接得到每个 token 的对应的计算量为 $8nh^2 + 16nh^2 = 24nh^2$。
2.3.1 计算量定性和定量结论
当隐藏维度 $h$ 比较大,且远大于序列长度 $s$ 时,则可以忽略一次项:
prefill阶段的计算量FLOPs可以近似为 $24nh^2*bs$。decode阶段每轮forward的计算量为 $24nh^2*b$,模型参数量为 $12nh^2$;每个 token 对应的计算量为 $24nh^2$。
因为,输入的 tokens 总数为 $bs$(即上下文总长度),即对于一个 token 存在等式: $\frac{24nh^2}{12nh^2} = 2$。所以,我们可以近似认为:在一次前向传播中,对于每个 token 和 每个模型参数,需要进行 $2$ 次浮点数运算,即一次乘法法运算和一次加法运算。
实际会有不到
2%的误差,主要是因为我们忽略了一些小算子的计算量。
一次迭代训练包含了前向传递和后向传递,后向传递的计算量是前向传递的 2 倍。因此,前向传递 + 后向传递的系数 $=1 + 2 = 3$ 。即一次迭代训练中,对于每个 token 和 每个模型参数,需要进行 $6$ 次浮点数运算。
有了上述训练和推理过程中计算量与参数量关系的结论。接下来,我们就可以估计一次迭代训练 GPT3-13B 所需要的计算量。对于 GPT3,每个 token,每个参数进行了 $6$ 次浮点数运算,再乘以参数量和总 tokens数就得到了总的计算量。GPT3 的模型参数量为 12850M,训练数据量 300B tokens。
计算结果和下表所示结果相符合。
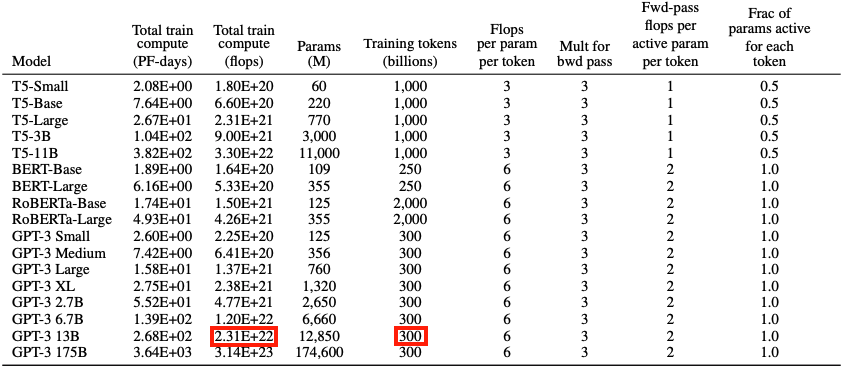
估算训练一个 transformer 模型所需的算力成本的公式可参考文章Transformer 估算 101。本章主要参考 Transformer Inference Arithmetic 以及 分析transformer模型的参数量、计算量、中间激活、KV cache。
这个表总结了常见大型语言模型(LLM)的参数数量、序列长度、批次大小、隐藏层大小、层数和每次前向推理的浮点操作数总量(FLOPs),FLOPs 以 T(万亿)为单位。
| Model | Parameters | Sequence Length | Batch Size | Hidden Size | Number of Layers | FLOPs (prefill) |
|---|---|---|---|---|---|---|
| GPT-3 (175B) | 175B | 2048 | 8 | 12288 | 96 | ~7.0 × 10³ T FLOPs |
| GPT-3 (13B) | 13B | 2048 | 8 | 4096 | 40 | ~4.4 × 10² T FLOPs |
| BERT-Large | 345M | 512 | 8 | 1024 | 24 | ~2.4 × 10¹ T FLOPs |
| T5-11B | 11B | 512 | 8 | 1024 | 24 | ~1.4 × 10² T FLOPs |
| LLaMA-13B | 13B | 2048 | 8 | 5120 | 40 | ~4.4 × 10² T FLOPs |
| PaLM-540B | 540B | 2048 | 8 | 16384 | 96 | ~6.7 × 10⁴ T FLOPs |
| ChatGPT (GPT-4) | 175B | 2048 | 8 | 12288 | 96 | ~7.0 × 10³ T FLOPs |
三 显存占用量分析
3.1 训练过程中显存占用量计算
中间激活:前向传播计算过程中,前一层的输出就是后一层的输入,相邻两层的中间结果也是需要 gpu 显存来保存的,中间结果变量也叫激活内存,值相对很小。
在模型训练过程中,设备内存中除了需要模型权重之外,还需要存储中间变量(激活)、梯度和化器状态动量,后者显存占用量与 batch size 成正比。
在模型训练过程中,存储前向传播的所有中间变量(激活)结果,称为 memory_activations,用以在反向传播过程中计算梯度时使用。而模型中梯度的数量通常等于中间变量的数量,所以 memory_activations = memory_gradients。
假设 memory_modal 是指存储模型所有参数所需的内存、memory_optimizer 是优化器状态变量所需内存。综上,模型训练过程中,显存占用量的理论计算公式为:
total_memory = memory_modal + 2 * memory_activations + memory_optimizer
值得注意的是,对于 LLM 训练而言,现代 GPU 通常受限于内存瓶颈,而不是算力。因此,激活重计算 (activation recomputation,或称为激活检查点 (activation checkpointing) ) 就成为一种非常流行的以计算换内存的方法。
激活重计算主要的做法是重新计算某些层的激活而不是把它们存在 GPU 内存中,从而减少内存的使用量,内存的减少量取决于我们选择清除哪些层的激活。
3.2 推理过程中显存占用量计算
深度学习模型推理任务中,占用 GPU 显存的主要包括三个部分:模型权重、输入输出以及中间激活结果。(该结论来源论文)因此,LLM 显存占用可分为 3 部分:
1,存储模型权重参数所需的显存计算公式(params 是模型参数量,参数类型为 fp16):
2,中间激活显存占用(额外开销)
和模型训练需要存储前向传播过程中的中间变量结果不同,模型推理过程中并不需要存储中间变量,因此推理过程中涉及到的中间结果内存会很小(中间结果用完就会释放掉),一般指相邻两层的中间结果或者算子内部的中间结果,这里我们只考虑主要算子中最大的中间结果部分即可。
这里我们假设其占用的显存为 memory_intermediate,heads 数量用符号 $n_\text{head}$ 表示,假设输入数据的形状为 $[b,s]$。
- 每个 self-attention 头需要计算 Query 和 Key 的点积,每个头的 $QK^T$ 矩阵乘法的输入输出形状为 $[b, n_head, s, h//n_head] \times [b, n_head, h//n_head, s] \rightarrow [b, n_head, s, s]$,所以占用显存大小为 $2bs^2n_{head}$;
mlp块中,第一个线性层的输出结果形状为 $[b, s, 4h]$,所以占用显存大小为 $8bsh$。
计算 MHA和 MLP 的 memory_intermediate 的伪代码如下:
memory_intermediate of attention(qk^t output) = 2 * batch_size * n_head * square_of(sequence_length)
memory_intermediate of mlp(fc1 layer1 output) = 2 * batch_size * s * 4h
又因为一般 $h \gg s$,所以 memory_intermediate of mlp 远大于 memory_intermediate of attention。所以:
值得注意的是,根据经验,在模型实际前向传播过程中产生的这些额外开销(中间激活)通常控制在总模型参数内存的 20% 以内(只有 80% 的有效利用率)。
3,kv cache 显存占用
LLM 推理优化中 kv cache 是常见的方法,本质是用空间换时间。假设输入序列的长度为 $s$ ,输出序列的长度为 $o$,decoder layers 数目为 $n$,以 float16 来保存 KV cache,那么 KV cache 的峰值显存占用计算公式(不使用 GQA 优化)为:
上式,第一个 2 表示 K/V cache,第二个 2表示 float16 占 2 个 bytes。每个 token 的 kv 缓冲大小 $ = 4nh$,单位为字节 byte。
综上分析可知,llm 推理时,gpu 显存占用主要是:模型权重和 kv cahce,总显存消耗计算如下:
\(\begin{aligned}\text{inference\_memory} &\simeq [n(12h^2 + 13h) + Vh]*2 + 8bsh + 4nhb(s+o) \\ &\simeq 1.2 \cdot 24nh^2 + 4nhb(s+o)\end{aligned}\)
模型推理时,中间激活最大不会超过模型权重参数内存的 20%。当 $h$ 较大时,忽律掉一次项。
中间激活和 kv cache 显存和批次大小 $b$ 以及序列长度 $s$ 成正比,在 bs > 某个阈值时,占推理显存大头的是 kv cache。以 llama13b 为例分析,权重参数占用 26GB,当 b = 64, s = 512 时,输出序列长度 o = 512, kv cache 显存占用 = $4nhb(s+o) = 42,949,672,960\ bytes \simeq 42GB$,是模型参数显存的 1.6 倍。
b的增加能带来近乎线性的throughput增加,llm 服务模块的调度策略就是动态调整批次大小,并尽可能让它最大。
3.3 显存占用计算的定性分析和定量结论
- 模型推理阶段,当输入输出上下文长度之和比较小的时候,占用显存的大头主要是模型参数,但是当输入输出上下文长度之和很大的时候,占用显存的大头主要是
kv cache。 - 每个
GPUkv cache显存所消耗的量和输入 + 输出序列长度成正比,和batch_size也成正比。 - 有文档指出,
13B的LLM推理时,每个token大约消耗1MB的显存。
以 A100-40G GPU 为例,llama-13b 模型参数占用了 26GB,那么剩下的 14GB 显存中大约可以容纳 14,000 个 token。在部署项目中,如果将输入序列长度限制为 512,那么该硬件下最多只能同时处理大约 28 个序列。
3.4 LLM 并发支持估算
以集群上的单节点 8 卡 V100 机器运行 llama-13b 模型为例,估算极端情况下聊天系统同时服务 10000 人并发所需要的节点数量。这里的极端情况是指每个请求的输入长度为 512、输出长度为 1536(即上下文长度为 2048)且没有 latency 要求。
LLaMA 系列模型配置文件中 “max_sequence_length”: 2048, 即代表预训练的 LLaMA 模型的最大 Context Window 只有
2048。另外,V100 卡的显存为 32GB。
结合前面的显存分析章节可知,k、v cache 优化中对于每个 token 需要存储的字节数为 $4nh$。
1,对 llama-13b 模型推理而言,使用 fp16 推理时,其模型参数实际占用显存量为 24.6GB(略小于理论参数显存 26),每个 token 大约消耗 1MB 的显存(其实是 kv cache 占用的缓冲),对于输入输出上下文长度(512+1536)和为 2048 的请求,其每个请求需要的显存是 2GB。这里对每个请求所需要显存的估算是没有计算推理中间结果所消耗显存(其比较小,可忽略),另外不同框架支持张量并行所需要的额外显存也各不相同,这里暂时也忽略不计。
- 在模型权重为
float16的情况下,支持的理论 batch 上限为 (32*8-24.6)/ 2 = 115.7。 - 在模型权重为
int8的情况下,支持的理论 batch 上限为 (32*8-24.6/2)/ 2 = 121.85。(deepspeed 框架不支持 llama 模型的 int8 量化)
以上是理论值即上限值,float16 权重的实际 batch 数量会小于 115.7,目前的 deepspeed 框架运行模型推理时实测 batch 数量只可以达到 $50$ 左右。
10000/50 = 200 (台 8 卡 V100 服务器)。
实际场景中的并发请求具有稀疏性,不可能每个请求都是 2048 这么长的上下文长度,因此实际上 200 台 8 卡 V100 服务器能服务的并发请求数目应该远多于 10000,可能是几倍。
2,对于 llama-65b 模型而言,其推理时,每个 token 大约消耗 2.5MB(估算的 $4nh = 4\ast 80\ast 8192 / (1024\ast 1024) = 2.5 \; \text{MB}$)的显存,因此,极限情况下每个请求需要的显存是 5GB。
- 在模型权重为 float16 的情况下,支持的理论 batch 上限为 (32 * 8 - 121.6)/ 5 = 26.88。
- 在模型权重为 int8 的情况下,支持的理论 batch 上限为 (32 * 8 - 121.6/2)/ 5 = 39.04。(deepspeed 框架不支持 llama 模型的 int8 量化)
另外,如果输入能量化为 int8 数据类型,理论上支持的 batch 数量会翻倍。
支持并发数理论估算
这里的并发估算的请求长度是按照模型支持的最大上下文长度来估算的,且没有 latency 要求。
\[最大并发数 = \frac{单卡显存 \times 卡数 - 模型参数显存占用(量化前/后)} {单个请求最大显存占用} \\ 单个请求最大显存占用 = \text{每个 token 的 kv cache 占用显存} \times \text{max\_sequence\_length} \\\]四 结论
对于典型自回归 llm,假设 decoder layers 层数为 $n$,隐藏层大小(Embedding 向量维度)为 $h$,输入输入数据形状为 $[b,s]$。当隐藏维度 $h$ 比较大,且远大于序列长度 $s$ 时,则参数量和计算量的估算都可以忽略一次项,则有以下关于参数量、计算量和显存占用计算分析结论。
一些定性结论:
- 参数量和输入序列长度无关。$\text{Parmas} = 12nh^2$。
- 每个
token对应的 $\text{Flops} = 24nh^2$,计算量随序列长度呈线性增长。其中 $\text{Prefill flops} = 24nh^2\cdot bs$;每轮 decode 的计算量 $\text{Decode flops} = 24nh^2\cdot b$。 - 每个
token的 kv cache 占用显存大小是 $4nh$,kv cache显存占用量随(输入 + 输出序列长度)以及批量大小batch_size呈线性增长。kv cache 显存占用量 $= b(s+o)h\cdot n \cdot 2\cdot 2 = 4nh\cdot b(s+o)$,单位为字节byte。 self-attention的内存和计算复杂度随序列长度 $s$ 呈二次方增长。注意力输出矩阵 $O = \text{softmax}(QK^T)V$ 要求 $O(N^2d)$ 的 FLOPs,并且除了输入和输出内存之外,需要额外的 $O(N^2)$ 内存。
定量结论(近似估算):
- 一次迭代训练中,对于每个 token 和 每个模型参数,需要进行 6 次浮点数运算。
- 随着模型变大,
MLP和Attention层参数量占比越来越大,最后分别接近66%和33%。 - 有文档指出,
13B的LLM推理时,每个token大约消耗1MB的显存。
参考资料
- Transformer Deep Dive: Parameter Counting
- Transformer Inference Arithmetic
- Estimating memory requirements of transformer networks
- Formula to compute approximate memory requirements of Transformer models
- How continuous batching enables 23x throughput in LLM inference while reducing p50 latency
- 如何估算transformer模型的显存大小
- 大模型推理性能优化之KV Cache解读
- 如何生成文本: 通过 Transformers 用不同的解码方法生成文本
- 分析transformer模型的参数量、计算量、中间激活、KV cache
- github-LLM-Viewer