理解 triton 内核教程 3
Categories: Hpc
1. LN 原理
LN 作用是减少了不同特征之间的依赖关系,可以使得模型训练更加稳定,收敛更快,并提高了模型的泛化能力。Batch Norm 和 Layer Norm 的区别一句话总结就是 bn 是切特征,ln 是切样本。
BN: 对于每个特征维度,计算它在整个批次中的均值和标准差,然后对该特征进行归一化。LN: 对每个样本单独计算其所有特征的均值和标准差,然后在该样本内进行归一化。
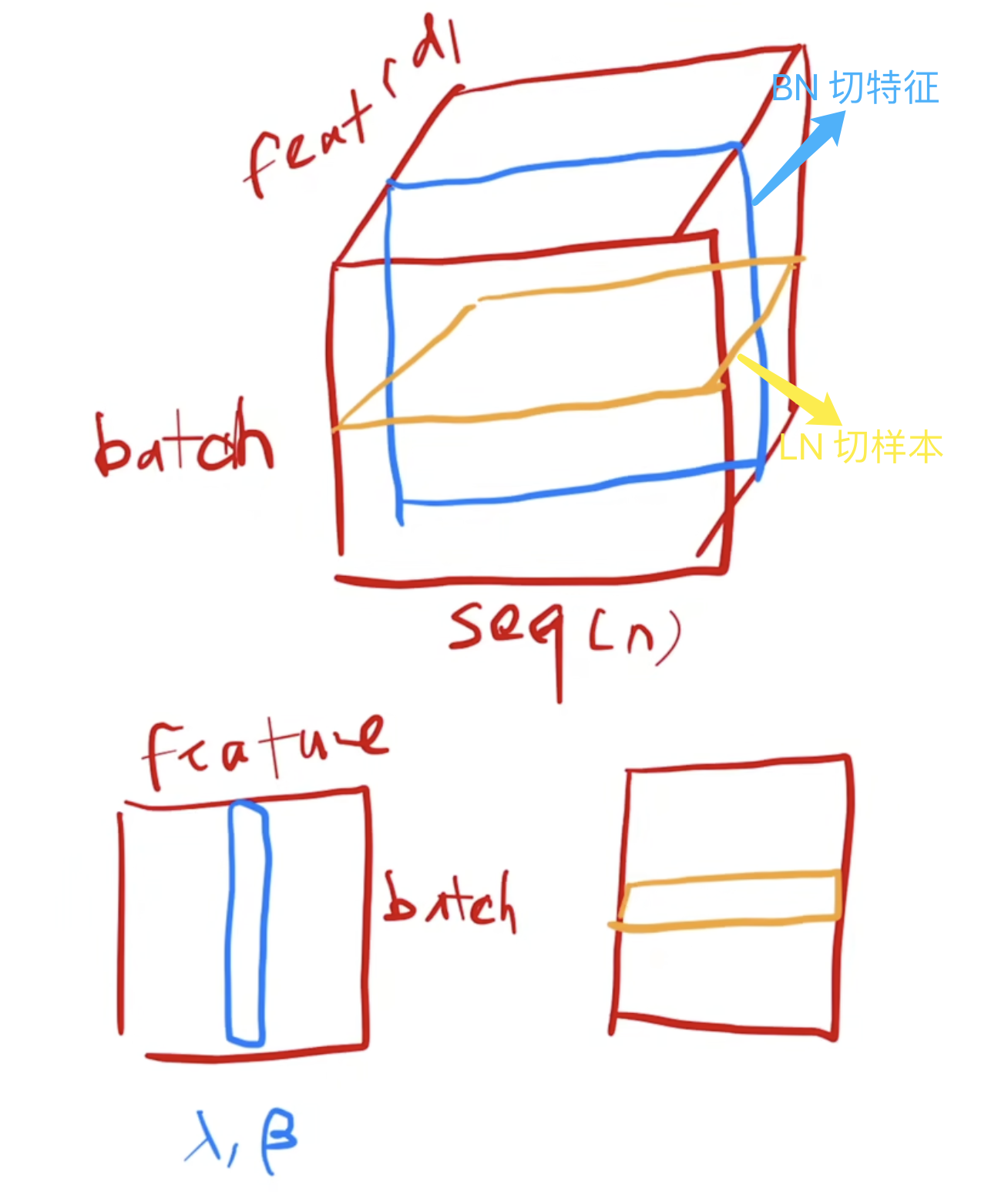
Layer Norm 操作具体来说,它接受一个向量 $\boldsymbol{x}$ 作为输入,输出一个与之形状相同的向量 $\boldsymbol{y}$。归一化通过对 $\boldsymbol{x}$ 减去均值并除以标准差来实现。完成归一化后,再应用具有可学习参数 $\boldsymbol{\gamma}$(权重)和 $\boldsymbol{\beta}$(偏置)的线性变换。前向传播过程可以表示如下:
\(y = \frac{x - E[x]}{\sqrt{(Var(x) + \epsilon)}} * \gamma + \beta\)
其中 $\epsilon$ 是一个很小的常数添加到分母以实现数值稳定性。
2 其他 Norm 介绍
2.1 种类介绍
下述对沿着哪个维度计算均值的描针对的是视觉领域的 4D 张量 $\text{[N, C, H, W]}$:
BatchNorm:batch方向做归一化,算 NHW 的均值,对小 batch size 效果不好;BN 主要缺点是对 batch size 的大小比较敏感,由于每次计算均值和方差是在一个 batch 上,所以如果 batchsize 太小,则计算的均值、方差不足以代表整个数据分布。LayerNorm:channel方向做归一化,算 CHW 的均值,主要对 RNN 作用明显;InstanceNorm:一个 channel 内做归一化,算H*W的均值,用在风格化迁移;因为在图像风格化中,生成结果主要依赖于某个图像实例,所以对整个batch归一化不适合图像风格化中,因而对HW做归一化。可以加速模型收敛,并且保持每个图像实例之间的独立。GroupNorm:将 channel 方向分 group,然后每个 group 内做归一化,算(C//G)HW的均值;这样与 batch size 无关,不受其约束。 SwitchableNorm是将BN、LN、IN结合,赋予权重,让网络自己去学习归一化层应该使用什么方法。
2.2 BN、LN、IN 和 GN 计算上的区别
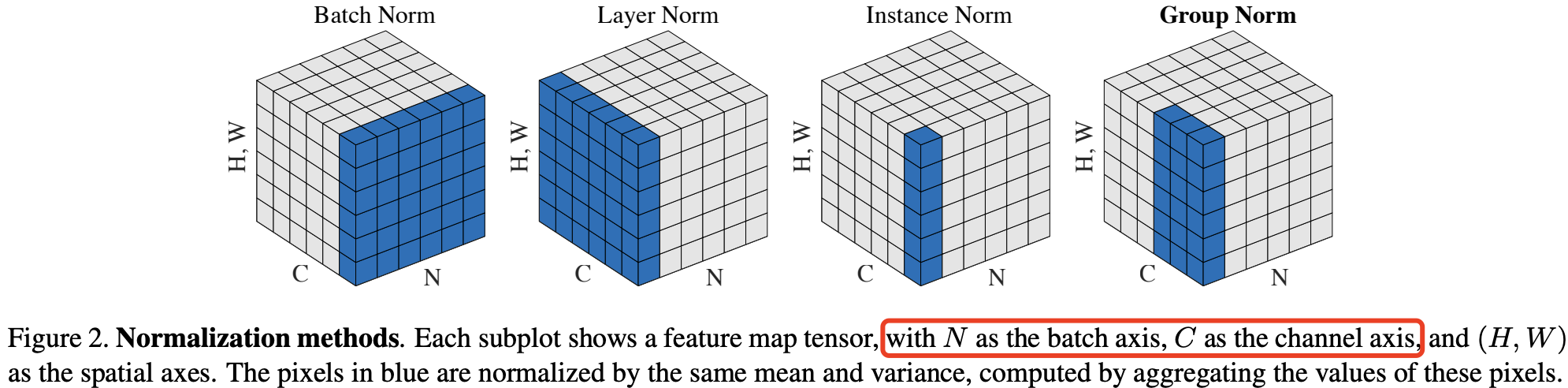
特征归一化方法家族,包括 BN(批归一化)、LN(层归一化)、IN(实例归一化)和 GN(组归一化),都执行如下计算:
\[\hat{x}_i = \frac{x_i - \mu_i}{\sigma_i}. \tag{1}\]其中,$x$ 是由某一层计算出的特征,$i$ 代表特征的索引。
对于 2D 图像来说,$i = (i_N, i_C, i_H, i_W)$ 是一个 4D 向量,按照 $(N, C, H, W)$ 的顺序索引特征,其中 $N$ 代表批次维度,$C$ 代表通道维度,$H$ 和 $W$ 代表空间高度和宽度。
公式(1)中的 $\mu$ 和 $\sigma$ 分别是均值和标准差,通过以下方式计算:
\[\mu_i = \frac{1}{m} \sum_{k \in S_i} x_k, \quad \sigma_i = \sqrt{\frac{1}{m} \sum_{k \in S_i} (x_k - \mu_i)^2 + \epsilon}, \tag{2}\]其中 $\epsilon$ 为一个小常数。(S_i) 是用于计算均值和标准差的像素集合, (m) 是该集合的大小。不同特征归一化方法的主要区别在于如何定义集合 (S_i) (公式 2 所示),对于 2D 图像的具体定义如下:
在批归一化(Batch Norm, BN)[26] 中,集合 (S_i) 定义为:
\[S_i = \{k \mid k_C = i_C \}\]其中 (i_C) (以及 (k_C))表示 (i) (以及 (k))沿着通道维度(C 轴)的子索引。这意味着具有相同通道索引的像素被一同归一化,换句话说,$\text{BN}$ 对每个通道沿着 (N, H, W) 轴计算均值和标准差。
在层归一化(Layer Norm, LN)[3] 中,集合定义为:
\[S_i = \{k \mid k_N = i_N \}\]这意味着 $\text{LN}$ 对每个样本沿着 (C, H, W) 轴计算均值和标准差。
在实例归一化(Instance Norm, IN)[61] 中,集合定义为:
\[S_i = \{k \mid k_N = i_N, k_C = i_C \}\]这意味着 $\text{IN}$ 对每个样本的每个通道沿着 (H, W) 轴计算均值和标准差。下图显示了 BN、LN 和 IN 之间的关系。
3. LN 前向传播内核
结合前面向量相加、softmax 算子、矩阵乘法内核的实现,我们可以自行实现 LN 层的内核代码了。输入 x 是二维的,因此计算是逐行进行的。值得说明的是,每行的元素数量(N)是比较多的,一般超过 BLOCK_SIZE,因此需要对一行元素的数量分块计算,在 kernel 内用 for 循环遍历。
import torch
import triton
import triton.language as tl
@triton.jit
def _layer_norm_fwd_fused(
X, # pointer to the input
Y, # pointer to the output
W, # pointer to the weight
B, # pointer to the bias
Mean, # pointer to the mean
Rstd, # pointer to the 1/std
stride, # how much to increase the pointer when moving by 1 row
N, # number of columns in X
eps, # epsilon to avoid division by zero
BLOCK_SIZE: tl.constexpr,
):
# 一行的元素数量 N 一般远超 BLOCK_SIZE,故需要对 N 进行分块计算
row_idx = tl.programs(0)
X += row_idx * stride
Y += row_idx * stride
# 计算均值
mean = 0
_mean = tl.zeros([BLOCK_SIZE], dtype=tl.float32)
for off in range(0, N, BLOCK_SIZE):
col_offsets = off + tl.arange(0, BLOCK_SIZE)
x_sub = tl.load(X + col_offsets, mask = col_offsets<N, other=0.).to(tl.float32)
_mean += x_sub
mean = tl.sum(_mean, axis = 0) / N
# 计算方差
_var = tl.zeros([BLOCK_SIZE], dtype=tl.float32)
for off in range(0, N, BLOCK_SIZE):
col_offsets = off + tl.arange(0, BLOCK_SIZE)
x = tl.load(X + col_offsets, mask = col_offsets<N, other=0.).to(tl.float32)
x = tl.where(cols < N, x - mean, 0.)
_var += x*x
var = torch.sum(_var, axis = 0) / N
rstd = 1 / tl.sqrt(var + eps)
# 写均值和方差到内存
tl.store(Mean + row_idx, mean)
tl.store(Rstd + row_idx, rstd)
# 算LN
for off in range(0, N, BLOCK_SIZE):
col_offsets = off + tl.arange(0, BLOCK_SIZE)
mask = col_offsets < N
w = tl.load(W + col_offsets, mask=mask)
b = tl.load(B + col_offsets, mask=mask)
x = tl.load(X + col_offsets, mask = mask, other=0.).to(tl.float32)
x_hat = (x - mean) * rstd
y = x_hat*w + b
# 将LN写到输出内存地址
tl.store(Y + col_offsets, y, mask=mask)
内核实现好了之后,调用内核的函数也好编写了,代码如下:
class LayerNorm(torch.autograd.Function):
@staticmethod
def forward(ctx, x, normalized_shape, weight, bias, eps):
# allocate output
y = torch.empty_like(x)
# reshape input data into 2D tensor
x_arg = x.reshape(-1, x.shape[-1])
M, N = x_arg.shape
mean = torch.empty((M, ), dtype=torch.float32, device=x.device)
rstd = torch.empty((M, ), dtype=torch.float32, device=x.device)
# Less than 64KB per feature: enqueue fused kernel
MAX_FUSED_SIZE = 65536 // x.element_size()
BLOCK_SIZE = min(MAX_FUSED_SIZE, triton.next_power_of_2(N))
if N > BLOCK_SIZE:
raise RuntimeError("This layer norm doesn't support feature dim >= 64KB.")
# heuristics for number of warps
num_warps = min(max(BLOCK_SIZE // 256, 1), 8)
# enqueue kernel
_layer_norm_fwd_fused[(M, )]( # grid 形状为一维,大小就是输入 x 的行数
x_arg, y, weight, bias, mean, rstd, #
x_arg.stride(0), N, eps, #
BLOCK_SIZE=BLOCK_SIZE, num_warps=num_warps, num_ctas=1)
ctx.save_for_backward(x, weight, bias, mean, rstd)
ctx.BLOCK_SIZE = BLOCK_SIZE
ctx.num_warps = num_warps
ctx.eps = eps
return y
内核函数测试代码如下所示:
layer_norm = LayerNorm.apply
def test_layer_norm(M, N, dtype, eps=1e-5, device='cuda'):
# create data
x_shape = (M, N)
w_shape = (x_shape[-1], )
weight = torch.rand(w_shape, dtype=dtype, device=device, requires_grad=True)
bias = torch.rand(w_shape, dtype=dtype, device=device, requires_grad=True)
x = -2.3 + 0.5 * torch.randn(x_shape, dtype=dtype, device=device)
dy = .1 * torch.randn_like(x)
# forward pass
y_tri = layer_norm(x, w_shape, weight, bias, eps)
y_ref = torch.nn.functional.layer_norm(x, w_shape, weight, bias, eps).to(dtype)
# compare
assert torch.allclose(y_tri, y_ref, atol=1e-2, rtol=0)
if __name__ == "__main__":
test_layer_norm(1151, 8192, torch.float16)