理解 triton 之基础知识
Categories: Hpc
一 tensor 知识
理解张量维度
在 PyTorch 中,张量的维度(或称为“秩”)决定了数据的结构和形状:
- 1D 张量:向量。例如,长度为 5 的向量 [1, 2, 3, 4, 5]。
- 2D 张量:矩阵。例如,形状为 (3, 4) 的矩阵。
- 3D 张量:通常用于 NLP,形状为 (batch_size, sequence_length, hidden_size)。
- 4D 张量:通常用于 CV,形状为 (batch_size, channels, height, width)。
在一个 $M$ 行 $N$ 列的二维数组中,$M$ 是第 0 维,即行数;$N$ 是第 1 维,即列数。那么怎么肉眼判断更复杂的张量数据维度呢,举例:
import torch
# 示例张量
tensor = torch.tensor([[[0.6238, -0.9315, 0.2173, 0.1954, -1.1565],
[0.4559, 0.1531, 0.4178, 1.0225, 0.5923],
[0.0499, 0.4024, -1.2547, -0.5042, -0.0231],
[-1.1253, 0.3145, 0.8796, 0.4516, -0.0915]],
[[1.5794, -0.6367, -0.2559, 0.1237, -0.1951],
[0.1012, 0.0357, -0.5699, 1.0983, -0.2084],
[-0.7019, 0.5872, 0.7736, 0.7423, -0.7894],
[-0.3248, -0.5316, 1.2029, 0.2852, -0.4565]],
[[-0.0073, 1.4143, -0.1859, -0.7211, -0.8652],
[-0.3173, -0.4816, 0.1174, -0.1554, 0.9385],
[0.1283, -0.6547, 0.3687, -0.1948, 0.7754],
[-0.2185, -1.0437, 1.5963, -0.3284, -0.3654]]])
判断规则:方括号 [ 的嵌套层数代表张量的维度。最外层括号的元素数量是第 0 维的大小,往内推。
以上述张量为例分析:
tensor([[[ 0.6238, -0.9315, 0.2173, 0.1954, -1.1565], ... ]])
- 最外层 [ 里有 3 个子列表 -> 第 0 维大小为 3。
- 第二层 [ 里有 4 个子列表 -> 第 1 维大小为 4。
- 第三层 [ 里有 5 个元素 -> 第 2 维大小为 5。
因此,这个张量是 3 维张量,形状为 [3, 4, 5]。
理解 torch.matmul
torch.matmul 在处理多维张量时,会将最后两个维度视为矩阵执行矩阵乘法,其余的维度(必须相等)作为批次维度,逐个进行矩阵运算。
>>> A = torch.randn([4,5,9])
>>> B = torch.randn([4,9,5])
>>> C = torch.matmul(A, B)
>>> C.shape
torch.Size([4, 5, 5])
理解 dim 参数
dim 参数在 pytorch 函数中的定义指沿着 dim 这个维度进行操作:求和/求平均/求累加,以及删除、增加指定 dim。如 x 的 shape 为 [2, 5, 3],则:
dim = 0,即沿着具有 2 个元素的那个维度/轴进行操作dim = 1,即沿着具有 5 个元素的那个维度/轴进行操作dim = 2,即沿着具有 3 个元素的那个维度/轴进行操作
再看具体示例:
>>> x = torch.randint(1, 10, [2,5,3], dtype=torch.float32)
>>> x
tensor([[[8., 1., 6.],
[1., 5., 9.],
[5., 7., 1.],
[5., 1., 2.],
[8., 4., 4.]],
[[3., 3., 7.],
[7., 4., 3.],
[7., 7., 5.],
[8., 3., 9.],
[1., 1., 8.]]])
>>> x.shape
torch.Size([2, 5, 3])
# 如执行 y = torch.mean(x, dim = 0),则 y[0,0] = (x[0, 0, 0] + x[1, 0, 0]) / 2 = (8. + 3.) / 2 = 5.5; y[2, 2] = (x[0, 2, 2] + x[1, 2, 2]) = (1. + 5.) / 2 = 3.0
>>> y = torch.mean(x, dim = 0)
>>> y
tensor([[5.5000, 2.0000, 6.5000],
[4.0000, 4.5000, 6.0000],
[6.0000, 7.0000, 3.0000],
[6.5000, 2.0000, 5.5000],
[4.5000, 2.5000, 6.0000]])
# 如执行 y = torch.mean(x, dim = 2), 则 y[1, 4] = (x[1, 4, 0] + x[1, 4, 1] + x[1, 4, 2]) / 3
>>> y = torch.mean(x, dim = 2)
>>> y
tensor([[5.0000, 5.0000, 4.3333, 2.6667, 5.3333],
[4.3333, 4.6667, 6.3333, 6.6667, 3.3333]])
规约操作
规约操作(Reduction Operation)是指将多元素的输入数据按某种规则缩减为单一结果的操作。常见的规约操作包括 求和、求最大值、求最小值、求均值等。这些操作广泛应用于数据处理、并行计算和深度学习中,用于简化大量数据或归纳数据特性。
在深度学习中,规约操作通常用于对张量(tensor)数据进行分组聚合计算,表现结果就是会进行维度压缩。例如,某些神经网络层的输出可能需要通过规约操作进行归一化,或在损失函数的计算中将多个样本的损失值规约为一个标量。
Pytorch 中常用的规约算子有:
torch.sum:按指定维度对张量元素求和,没有指定维度就对所有元素求和。torch.prod:按指定维度对元素求积。torch.mean:按指定维度对张量元素求均值。torch.max:按指定维度对张量元素求最大值。torch.min:按指定维度对张量元素求最小值。torch.cumsum按指定维度计算累积和。torch.argmax和torch.argmin:分别返回最大值和最小值的索引。torch.all:按指定维度检查所有元素是否为 True。torch.any:按指定维度检查是否存在 True 元素。
1,torch.mean 函数用于计算张量沿指定维度的平均值。其基本语法和参数解释如下:
torch.mean(input, dim, keepdim=False, *, dtype=None) -> Tensor
input:输入张量。dim:沿哪个维度计算平均值。可以是单个整数或整数元组。keepdim:是否保留被缩减的维度。默认为 False。dtype:输出张量的数据类型。
- 从计算过程理解:沿着(跨) dim 进行操作(算均值)。
- 常规矩阵操作的 2D 张量,dim = 0 表示跨行操作,即对每一列中的所有元素进行均值计算。
- NLP 领域的 3D 张量
(batch_size, sequence_length, embedding_size),dim = 2表示跨嵌入层维度算均值,对于每个 (batch, sequence) 位置,计算嵌入维度上的均值,如创建一个形状为 (4, 16, 4) 的 3D 张量计算位置 (0, 0, :) 的均值 $\text{mean}(x[0, 0:]) = \frac{x[0,0,0] + x[0,0,1] + x[0,0,2] + x[0,0,3]}{4}$。 - CV 领域的 4D 张量
(batch_size, channels, height, width),dim = 0表示跨 batch_size 维度上计算均值,对一个批次中的所有样本进行平均。如创建一个形状为 (2, 3, 3, 3) 的 4D 张量,计算位置 (0, 0, 0) 的均值 = $\text{mean}(x[:, 0, 0, 0]) = \frac{x[0, 0, 0, 0] + x[1, 0, 0, 0]}{2}$。
- 从输出张量的形状理解:
- NLP 领域的 3D 张量,dim = 2,输出张量的形状去掉这个 dim 维度,得到输出张量形状为
(batch_size, sequence_length)。 - CV 领域的 4D 张量,dim = 0,输出张量形状为
(channels, height, width)。
- NLP 领域的 3D 张量,dim = 2,输出张量的形状去掉这个 dim 维度,得到输出张量形状为
2,torch.sum 沿着指定维度求和。
>>> x = torch.randn([4,5])
>>> x
tensor([[ 1.1141, 1.7091, -0.5543, 0.3417, -0.0838],
[-0.6697, -0.3165, 0.3772, -0.4377, -0.9850],
[-1.3976, 1.3172, -0.6791, 0.1030, -0.5817],
[ 0.3079, -0.5911, 1.2357, -1.0891, 0.8422]])
>>> x.sum(dim=0)
tensor([-0.6453, 2.1187, 0.3796, -1.0821, -0.8082])
>>> x.sum(dim=1)
tensor([ 2.5269, -2.0317, -1.2381, 0.7056])
当 dim = 0 时,就是沿着 dim = 0即 x 轴进行累加,sum 函数为规约函数会压缩维度,所以x.sum(dim=0) 结果为 tensor([-0.6453, 2.1187, 0.3796, -1.0821, -0.8082]),形状为 [5]。
3,torch.cumprod 沿着 dim 维度计算累积。min() 沿着指定 dim 找
>>> x = torch.Tensor([ # shape is [2, 5]
... [2,3,4,5,6],
... [9,8,7,6,5,]
... ])
>>> print(torch.cumprod(x, dim = 0))
tensor([[ 2., 3., 4., 5., 6.],
[18., 24., 28., 30., 30.]])
>>> print(torch.cumprod(x, dim = 1)) # output shape is [2, 5]
tensor([[2.0000e+00, 6.0000e+00, 2.4000e+01, 1.2000e+02, 7.2000e+02],
[9.0000e+00, 7.2000e+01, 5.0400e+02, 3.0240e+03, 1.5120e+04]])
>>> torch.min(x, dim = 0) # output shape is [5]
torch.return_types.min(
values=tensor([2., 3., 4., 5., 5.]),
indices=tensor([0, 0, 0, 0, 1]))
>>> print(torch.max(x, dim = 1)) # output shape is [2]
torch.return_types.max(
values=tensor([6., 9.]),
indices=tensor([4, 0]))
>>> torch.mean(x, dim = 0, keepdim = True) # output shape is [1, 5]
tensor([[5.5000, 5.5000, 5.5000, 5.5000, 5.5000]])
二 cuda 基础
矩阵元素指针算术
为了访问矩阵中的特定元素,使用指针算术计算其线性地址。对于矩阵 $A$ 形状为 $(M, K)$,元素 $A[m, k]$ 的线性地址计算如下:
\[\text{Address}(A[m, k]) = A_{\text{ptr}} + m \times K + k\]其中:
- $A_{\text{ptr}}$ 是矩阵 $A$ 的起始指针(即 A[0,0] 的地址)。
- $m \times K$ 是跳过前 $m$ 行的元素数量。
- $k$ 是当前行中跳过的元素数量。
子块地址计算方法:
对于矩阵 $A$ 形状为 $(M, K)$,元素顺序为:
\[A = \begin{bmatrix} A[0,0] & A[0,1] & \dots & A[0,K-1] \\ A[1,0] & A[1,1] & \dots & A[1,K-1] \\ \vdots & \vdots & \ddots & \vdots \\ A[M-1,0] & A[M-1,1] & \dots & A[M-1,K-1] \end{bmatrix}\]内存中的存储顺序:
\[A[0,0], A[0,1], \dots, A[0,K-1], A[1,0], A[1,1], \dots, A[1,K-1], \dots, A[M-1,K-1]\]在分块矩阵乘法中,矩阵被划分为多个子块。每个子块由其在行和列方向上的起始索引定义。矩阵子块加载、存储和计算的伪代码:
# Do in parallel
for m in range(0, M, BLOCK_SIZE_M):
# Do in parallel
for n in range(0, N, BLOCK_SIZE_N):
acc = zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=float32)
for k in range(0, K, BLOCK_SIZE_K):
a = A[m : m+BLOCK_SIZE_M, k : k+BLOCK_SIZE_K]
b = B[k : k+BLOCK_SIZE_K, n : n+BLOCK_SIZE_N]
acc += dot(a, b)
C[m : m+BLOCK_SIZE_M, n : n+BLOCK_SIZE_N] = acc
- a_block 地址范围:从 m 到 m + BLOCK_SIZE_M,列索引范围 k: k + BLOCK_SIZE_K。对应的子块矩阵元素地址是二维的,假设矩阵存储是行连续的,则地址范围为 (A_ptr + m * K + k, A_ptr + (m + BLOCK_SIZE_M) * K + k + BLOCK_SIZE_K) -1。
- b_block 地址范围:B_ptr + k * N + n, B_ptr + (k + BLOCK_SIZE_K) * N + (n + BLOCK_SIZE_N) - 1。
如果是 triton 中实现上述地址的计算,对应代码为:
# 1,行块和列块 id,即第几个块
pid_m = tl.program_id(axis=0) # 这里的 pid_m 就是上面的 m 变量
pid_n = tl.program_id(axis=0)
# 2,行和列索引范围
# pid_m * BLOCK_SIZE_M 是块在行方向的起始行索引,加上 tl.arange(0, BLOCK_SIZE_M)[:, None] 生成的行偏移量。
offsets_m = pid_m + tl.arange(0, BLOCK_SIZE_M)[:, None]
# pid_n * BLOCK_SIZE_N 是块在列方向的起始列索引,加上 tl.arange(0, BLOCK_SIZE_N)[None, :] 生成的列偏移量。
offsets_n = pid_n + tl.arange(0, BLOCK_SIZE_N)[None,:]
acc = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
for k in range(0, K, BLOCK_SIZE_K):
offsets_ak = k + tl.arange(0, BLOCK_SIZE_K)[None,:]
offsets_bk = k + tl.arange(0, BLOCK_SIZE_K)[:, None]
# offsets_m * K:跳过前 offsets_m 行,每行有 K 个元素。
a_idx = A_ptr + offsets_m * K + offsets_ak
b_idx = B_ptr + offsets_bk * N + offsets_n
a_block = tl.load(a_idx, mask=(offsets_m < M) & (offsets_ak < K), other=0.0)
b_block = tl.load(b_idx, mask=(offsets_bk < K) & (offsets_n < N), other=0.0)
acc = tl.dot(a, b, acc=acc)
# offs_m * N:跳过前 offs_m 行,每行有 N 个元素。offsets_n:当前块负责的列偏移量。
c_idx = C_ptr + offsets_m * N + offsets_n
tl.store(c_ptr + c_idx, acc, mask = (offsets_m < M) & (offsets < N), other=0.0)
META['BLOCK_SIZE'] 表示每个块(block)的大小,这个值很重要,因为它直接影响到内核的并行性和性能。Pytorch 中行步幅通常等于列数。
网格、块和内核
不同的 grid 则可以执行不同的程序(即 kernel)。grid 定义了内核(kernel)执行的网格大小,即有多少个块(blocks)将被启动来执行一个内核,同时每个块包含 ‘BLOCK_SIZE’ 个线程(threads),一个 block 中的 thread 能存取同一块共享的内存。
与 cuda 编程把 thread 当作并行执行的基本单位不同,在 Triton 中,块 block 才是内核并行执行的基本单位,每个块负责处理任务的一个子集,通过合理划分块大小,可以充分利用 GPU 的并行计算能力。可以8通过配置 grid size 来决定块的数量,而块内的每个线程是隐式定义的,不需要像 CUDA 那样手动配置线程布局。在 triton 中 grid 定义 blocks 数量本质上是定义内核的并行执行范围。
triton 中共享内存的使用方法:
- 共享内存通过 tl.zeros 和 tl.atomic_add 等操作配合实现。
- 每个 Block 独立分配共享内存,互不干扰。共享内存只在当前块内的所有线程可见,块之间无法共享。
- 不同 SM 上的共享内存是完全独立的。
cuda 执行模型
在执行 CUDA 程序的时候,每个 SP(stream processor) 对应一个 thread,每个 SM(stream multiprocessor)对应一个 Block。
num_warps 概念作用
CUDA 采用单指令多线程(SIMT)架构来管理和执行线程,wrap 是 CUDA 编程模型中的基本执行单位,一般每 32 个线程为一组且被称为线程束(warp),在硬件 SIMD 单元上一起执行。
num_warps 变量则决定了每个线程块中要使用的 warp 数量。线程块中的线程数通常是 warp 数量的倍数,假如 num_warps 是 4,那么每个 block 会包含 4 个 warp,即 block_size = 128 个线程(4 * 32)。
num_warps 的作用:
- 并行度控制:num_warps 参数让开发者可以更灵活地控制每个线程块的并行度,进而影响并发性能。通过选择合适的 num_warps 值,能够在更好地利用 GPU 资源的同时,避免资源浪费。
- 硬件利用效率:在不同的 GPU 硬件上,选择适当的 warp 数量,可以有效提升 GPU 核心的利用率。例如,更多的 warp 可以更好地隐藏内存访问延迟,提高并行效率。
- 与共享内存和寄存器的平衡:Triton 中每个线程块都有一定的共享内存和寄存器资源,num_warps 会影响这些资源的分配。增大 num_warps 会增加并行线程数,但可能导致每个线程可用的共享内存或寄存器变少。选择合适的值,可以在并行度和资源利用之间取得平衡。
三 triton 基础
triton 定义
Triton 是一种用于并行编程的语言和编译器,它旨在提供一个基于 Python 的编程环境,帮助高效编写自定义的深度神经网络(DNN)计算核,并在现代 GPU 硬件上以最大吞吐量运行。
Triton 的编程在语法和语义上与 Numpy 和 PyTorch 非常相似。然而,作为低级语言,开发者需要注意很多细节,特别是在内存加载和存储方面,这对于在低级设备上实现高速计算非常关键。
Triton 定义:
- Intermediate Lauguge:基于 Python 的DSL
- tiled Neural Network Compute:面向 GPU 体系特点,自动分析和实施神经网络计算的分块
- Compiler:编译器
一句话总结:Triton 既是语言,也是编译器。
triton 特性
Triton 是关心分块(tile)的技术,和 pytorch 的输入是张量视图不同,triton 的操作对象是张量指针,其更关心张量布局和如何分块(影响 kernel 性能),使用 triton 编写 kernel 性能下限很高,且开发时间大大减少。Triton 有 3 个重要的特性:
- 粒度为
block(tile):更关心 block(即 SM 和 CUDA 的 block 不完全一样),而不是 grid、block、thread 这样严格而又复杂的线程组织结构。 - 优化 Pass: 借助一系列的优化 Pass,它可以达到和 cuBLAS 等算子库接近的水平。
- 和 pytorch 无缝衔接: 输入是 torch 张量指针。
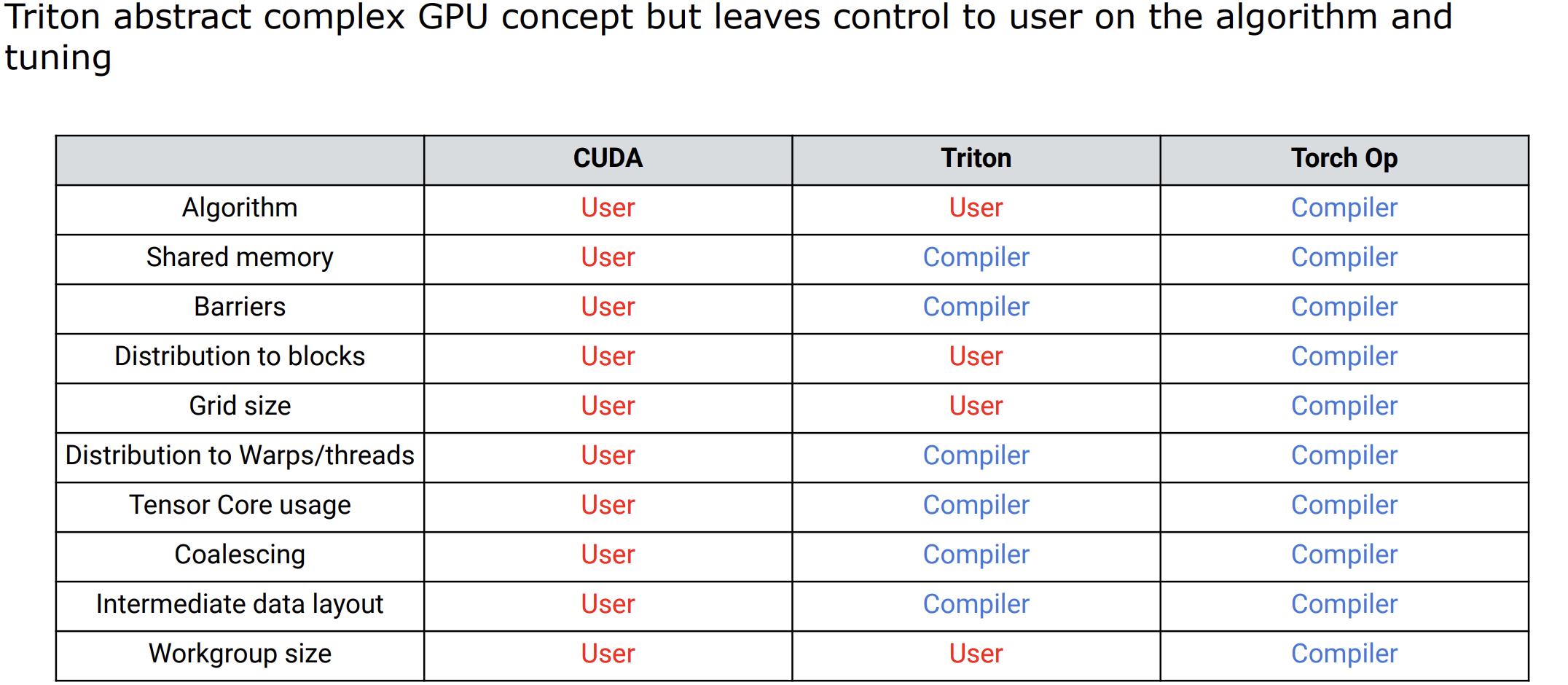
triton 算子和 torch eager 算子区别:
- triton 的操作对象是张量指针,torch 的输入是张量视图。
- 张量指针:关心张量布局,使用偏移量访问存储。
- 张量视图:关心张量形状,可能在储存上不连续。
- 通用算子领域,优化的 triton 算子性能可和 cuda 算子持平;在自定义算子、融合算子领域,短期内 triton 算子性能能更高。
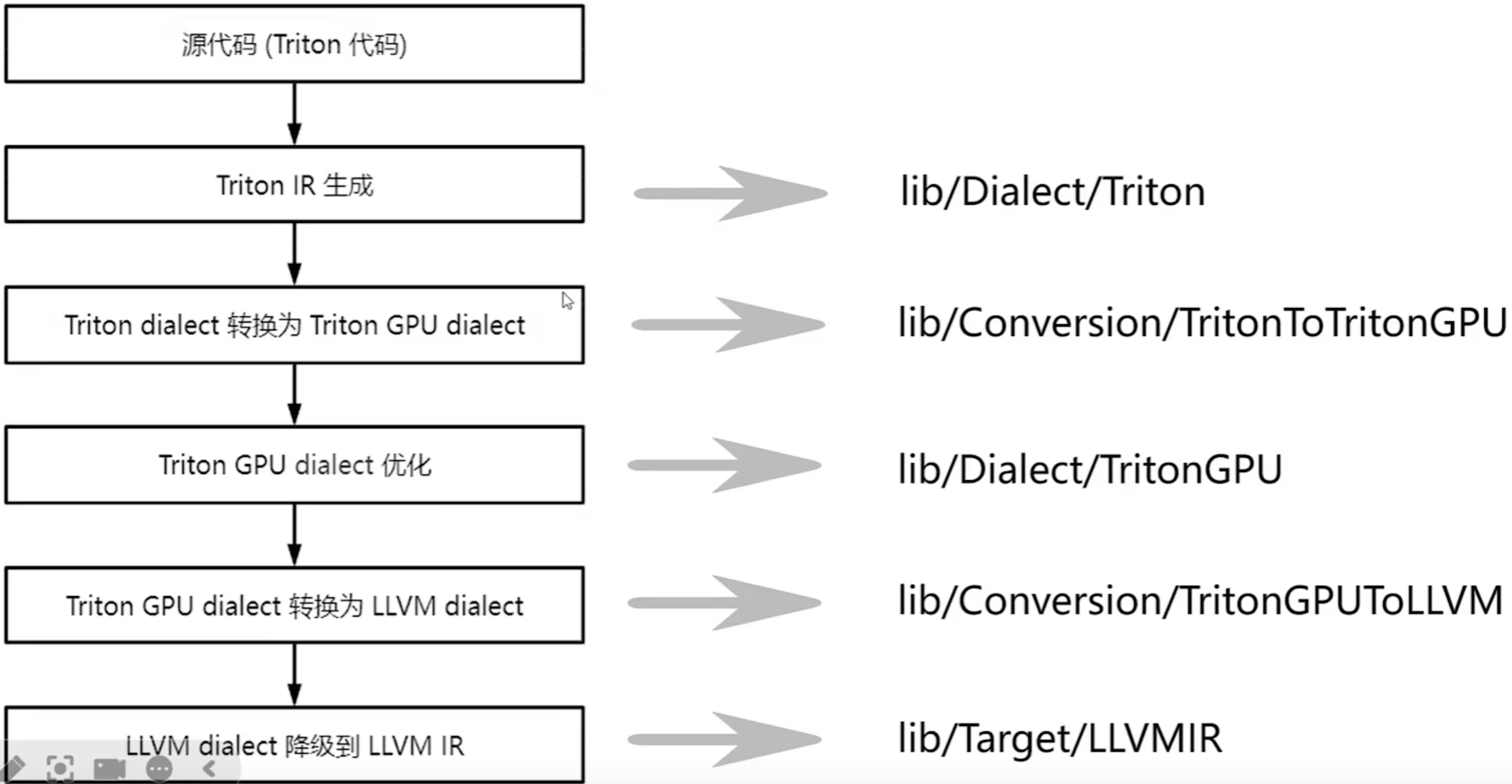
triton 编译过程
triton kernel -> triton IR -> LLVM IR -> PTX,最后配合 runtime 运行。
上述编译过程通过 @triton.jit 装饰器完成,具体来说是遍历提供的 Python 函数的抽象语法树(AST),并使用常见的 SSA 构建算法即时生成 Triton-IR。然后,编译器后端会简化、优化并自动并行化所产生的 IR 代码,再将其转换为高质量的 LLVM-IR,最后生成 PTX 并在 NVIDIA GPU 上执行。
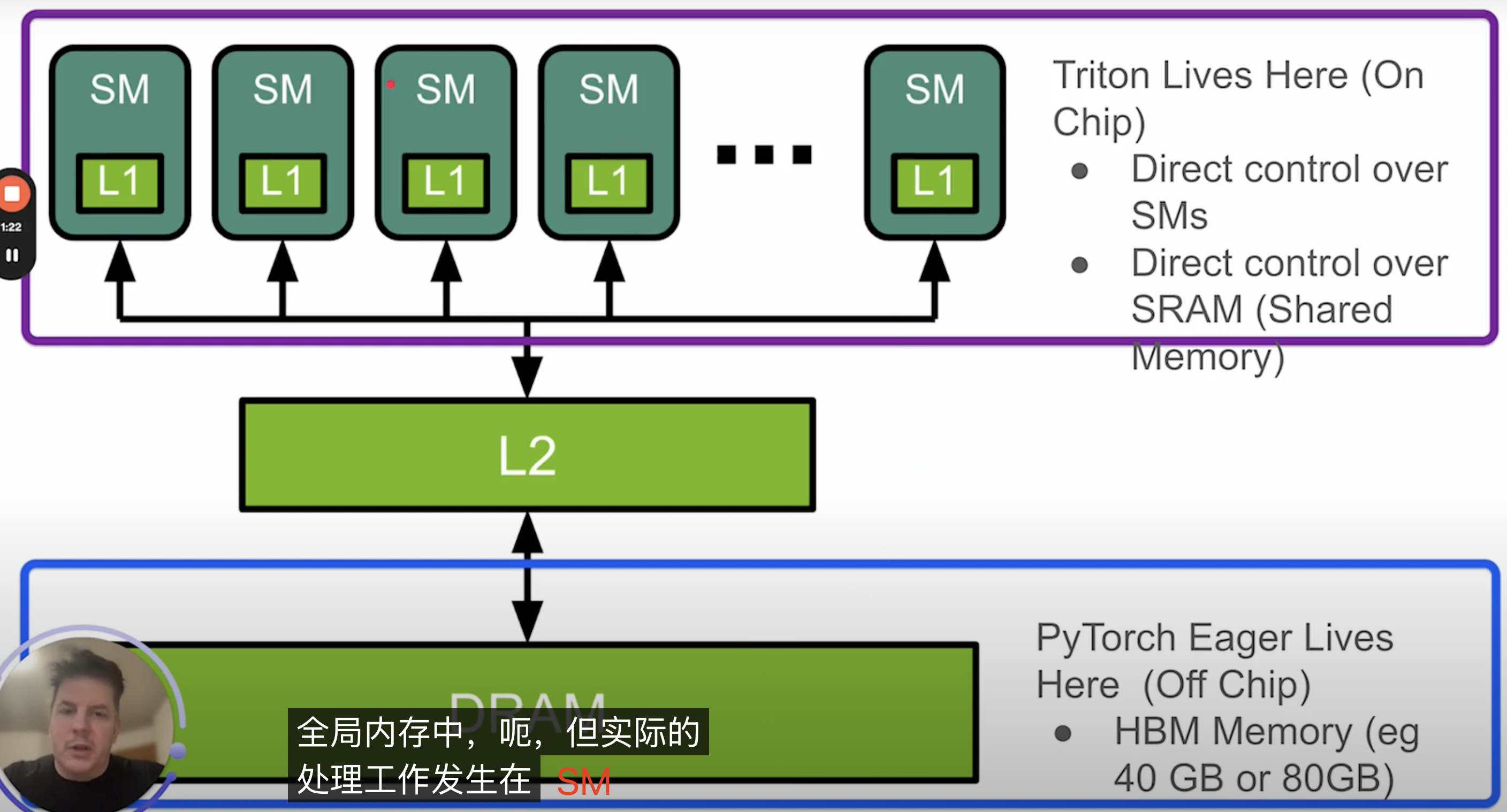
triton 操作 sram 和 pytorch eager 操作 hbm
triton 保留关键字
最新版的 triton3.0.0 有以下几种保留关键字(也称为元参数,kernel 调用的时候看到这些参数无需感到困惑,如果你设置了相关参数,编译器才会启动相关并行优化,没设置,就会自动抛弃这些关键字)。
RESERVED_KWS = ["num_warps", "num_stages", "num_ctas", "enable_fp_fusion", "grid", "maxnreg"]
num_warps: 用于设置 kernel 中线程束(warp)的数量。如果 kernel 的 num_warps = 8,那么 kernel 将会使用 256 个线程并行运行。num_stages:决定编译器为软件流水线循环(software-pipelining loops)分配的阶段数。主要用于在 SM80+ GPU(Ampere 架构)上执行矩阵乘法。(所谓流水线化,指的是允许多个循环的迭代同时进行,即后续迭代在前一个迭代尚未完成时就开始,每个迭代可以部分重叠执行以提高计算性能)num_ctas: 每个 SM(流多处理器)上并发执行的线程块(CTA)数量。grid: 控制 Triton 内核的 Grid 结构,代表 block 数目和维度。enable_fp_fusion:启用浮点运算融合,将多个浮点操作融合在同一流水线中执行,进一步提升性能,减少多次执行的开销;maxnreg:用于控制每个线程块(Block)所能使用的最大寄存器数量
Pytorch 与 Triton 中的地址计算对比
以下是图片中表格的 Markdown 源码:
| 步骤 | Python(PyTorch) | Triton |
|---|---|---|
| 矩阵存储方式 | 行优先(Row-Major Order) | 行优先(Row-Major Order) |
| 子块访问方式 | 使用切片操作 C[m:m+BLOCK_SIZE_M, n:n+BLOCK_SIZE_N] |
通过线性地址计算 C_ptr + offs_m*N + offs_n |
| 地址计算方法 | 自动管理,无需手动计算 | 手动计算线性地址,需考虑行优先存储和偏移量 |
| 并行化处理 | 通常在高级抽象层实现并行化 | 通过程序 ID(pid_m,pid_n) 映射到特定子块 |
| 掩码与边界处理 | 自动处理边界(切片超出范围会自动截断) | 需要手动处理边界,使用掩码 mask=(offs_m < M) & (x_k < K) |
| 数据加载与存储 | 直接访问子块数据 | 使用 t1.load 和 t1.store 进行数据加载与存储 |
| 子块累加与乘法 | 使用标准的矩阵乘法操作 | 使用 t1.dot 进行子块乘法并累加 |
triton 和 cuda 特性的对比
下述表格将 Triton 与 CUDA 的关键特性进行了对比,Triton 的编程模型在设计上的一大优势在于无需手动划分块,即 Block-wise 编程,Block 上面的归用户处理,Block 内部的归 Triton compiler 自动化处理。同时 Triton 在内存、TensorCore 以及向量化等方面都是自动进行的,可以简化一些 CUDA 编程中的手动优化过程,提供更多的自动化特性以提高开发效率和性能。
| CUDA | Triton | |
|---|---|---|
| Memory | Global/Shared/Local | Automatic |
| Parallelism | Threads/Blocks/Warps | Mostly Blocks |
| Tensor Core | Manual | Automatic |
| Vectorization | .8/.16/.32/.64/.128 | Automatic |
| Async SIMT | Support | Limited |
| Device Function | Support | Not Walable |
triton 的 autotune 用法
@triton.autotune 装饰器主要用于在运行时自动选择最佳的内核配置,以便在不同硬件或者不同输入尺寸(例如矩阵尺寸、序列长度等)下获得最优性能。它通过两个关键参数来实现这一目标:
1,configs 参数
- 作用:configs 是一个候选配置列表,每个候选配置都由一个字典和一些额外的运行参数构成。字典部分通常包含内核中用到的“meta 参数”(例如 BLOCK_M、BLOCK_N、BLOCK_K 等),而额外参数(如 num_warps、num_stages 等)则用于指定内核的调度和执行策略。
- 工作流程:当内核第一次运行时,Triton 会遍历 configs 中的每一个候选配置,并对每种配置进行短时间的性能评估。通过比较这些配置在实际工作负载下的执行时间,自动选择出性能最好的配置。之后,对于相同的工作负载(参见下文 key 参数),这个最佳配置会被缓存下来,后续调用就直接使用。
@triton.autotune(
configs=[
triton.Config({'BLOCK_M': 64, 'BLOCK_N': 64, 'BLOCK_K': 32}, num_warps=4, num_stages=2),
triton.Config({'BLOCK_M': 128, 'BLOCK_N': 128, 'BLOCK_K': 64}, num_warps=8, num_stages=3),
triton.Config({'BLOCK_M': 256, 'BLOCK_N': 256, 'BLOCK_K': 128}, num_warps=16, num_stages=4),
],
key=['M', 'N', 'K']
)
2,key 参数
- 作用:key 参数是一个列表,包含了若干字符串,这些字符串对应于内核函数中的参数(通常是通过 tl.constexpr 声明的)。这些参数的值会直接影响最佳配置的选择,因为不同的输入尺寸或问题规模可能需要不同的内核调度策略。
- 工作流程:在内核每次调用时,Triton 会根据 key 列表中指定的参数值生成一个“键”(key),用于在内部缓存中查找是否已经为这种输入选择了最优配置。如果没有,则 Triton 会对 configs 中的每个候选配置进行试验,选择出执行最快的一种,并将其与对应的 key 关联起来。之后对于同样的 key 值,直接复用之前选择的配置,避免重复调优带来的额外开销。
- 示例:在前面示例代码中,key=[‘M’, ‘N’, ‘K’] 意味着内核运行时会根据矩阵的行数 M、列数 N 和内积维度 K 来决定选择哪种配置。对于不同的矩阵尺寸,最佳的 BLOCK 尺寸和调度策略可能会不同,因此需要把这些参数作为区分的依据。
在 flashattentionv2 内核中的应用代码如下所示,完整的 flash_attention2_nopad_kernel 内核代码在这里:
configs_tma = [
triton.Config({'BLOCK_M_SIZE': BM, 'BLOCK_N_SIZE': BN}, num_stages=stages, num_warps=warps) \
for BM in [64, 128]\
for BN in [32, 64, 128]\
for warps in [4, 8, 16]\
for stages in [2, 3, 4, 6]\
]
def keep_tma(conf):
BLOCK_M_SIZE = conf.kwargs["BLOCK_M_SIZE"]
BLOCK_N_SIZE = conf.kwargs["BLOCK_N_SIZE"]
if (torch.cuda.get_device_capability()[0] == 9 and BLOCK_M_SIZE * BLOCK_N_SIZE < 128 * 128 and conf.num_warps == 8):
return False
return True
# key 参数列表(['B_Seqlen', 'HEAD_DIM'])的值会直接影响最佳配置的选择,因为不同的输入尺寸或问题规模可能需要不同的内核调度策略。
@triton.autotune(
configs=list(filter(keep_tma, configs_tma)),
key=['B_Seqlen', 'HEAD_DIM']
)
@triton.jit
def flash_attention2_nopad_kernel(
Q, K, V, O,
B_Start_Loc, B_Seqlen,
sm_scale, heads, num_kv_groups, # group of kv heads
stride_q_bs, stride_q_heads, stride_q_dim, # Q 的 strides
stride_k_bs, stride_k_heads, stride_k_dim, # K 的 strides
stride_v_bs, stride_v_heads, stride_v_dim, # V 的 strides
stride_o_bs, stride_o_heads, stride_o_dim,
HEAD_DIM: tl.constexpr, # head_dim dimension
BLOCK_M_SIZE: tl.constexpr, # BLOCK size of m_size dimension,即 Q 矩阵行数分成了m_size // BLOCK_M_SIZE 块,块大小是 BLOCK_M_SIZE
BLOCK_N_SIZE: tl.constexpr, # n_size dimension
):
num_warps 和 num_stages 性能参数的作用
1, num_warps
- 作用
- 并行度与延迟隐藏: num_warps 指定每个线程块(block)中启动的 warps 数量。更多的 warps 意味着在执行过程中可以调度更多线程,从而更好地隐藏内存访问延迟。
- 资源使用与调度开销:然而,过多的 warps 会占用更多的寄存器和共享内存资源,同时可能会使硬件调度器开销增大,影响总体效率。
- 设置建议
- 初始选择时,可以从硬件推荐的 warp 数量开始(通常
4~8个 warps 是一个较为常见的起点)。 - 针对不同问题规模和 GPU 架构,实验不同的 num_warps 组合。一般来说,对于计算密集型的 kernel,适当增加 warps 有助于提高利用率,而对于资源受限的 kernel,则需要谨慎增加。
- 初始选择时,可以从硬件推荐的 warp 数量开始(通常
2, num_stages
- 作用
- 软件流水线深度: num_stages 控制内核中指令流水线的阶段数。通过增加流水线阶段数,内核可以提前加载数据并将内存访问与计算重叠,从而隐藏内存访问延迟。
- 资源与同步开销:过多的流水线阶段虽然有助于延迟隐藏,但同时会增加寄存器压力和同步开销。如果流水线阶段设置得过高,可能反而影响性能。
- 设置建议
- 一般来说,
2~4个阶段比较常见。对于内存访问延迟较高或需要更多预取的情况,可以尝试增加阶段数;反之,如果内核计算量较大而内存延迟不是瓶颈,较少的流水线阶段可能更合适。 - 同样需要结合具体的内核特点和 GPU 架构,通过实验找到一个平衡点。
- 一般来说,