Sinusoida 位置编码详解

Categories: Transformer

一 Sinusoidal 位置编码

1.1 位置编码概述

不同于 RNN、CNN 等模型，对于 Transformer 模型来说，位置编码的加入是必不可少的，因为纯粹的 Attention 模块是无法捕捉输入顺序的，即无法区分不同位置的 Token。

简单来说，位置编码的意义是用于表示序列中某个元素的位置，它为每个位置分配一个独特的表示。在 Transformer 模型中，不使用像索引这样的单一数值来表示元素的位置有很多原因。对于较长的序列，索引的数值可能会非常大。如果将索引归一化到 0 到 1 之间，对于长度不同的序列，这种归一化方法会导致问题，因为它们的归一化方式不一致。

Transformer 模型采用了一种巧妙的位置信息编码方法，其中每个位置或索引都映射到一个向量，向量大小为 $d_\text{model}$。因此，位置编码层的输出是一个矩阵，其中矩阵的每一行表示一个序列元素的编码，该编码包括了该元素的位置信息，这种位置编码方式称为 Sinusoidal 位置编码。下图展示了一个仅编码位置信息的矩阵示例。

PE demo

正弦函数

理解 transformer 模型提出的位置信息绝对编码算法之前，先对正弦函数做一个快速回顾（余弦函数特性差不多）。

在数学中，正弦（英语：sine、缩写sin）是一种周期函数，是三角函数的一种。它的定义域是整个实数集，值域是 $[-1, 1]$。它是周期函数，其最小正周期为 $2\pi$ ($360^{\circ}$)。

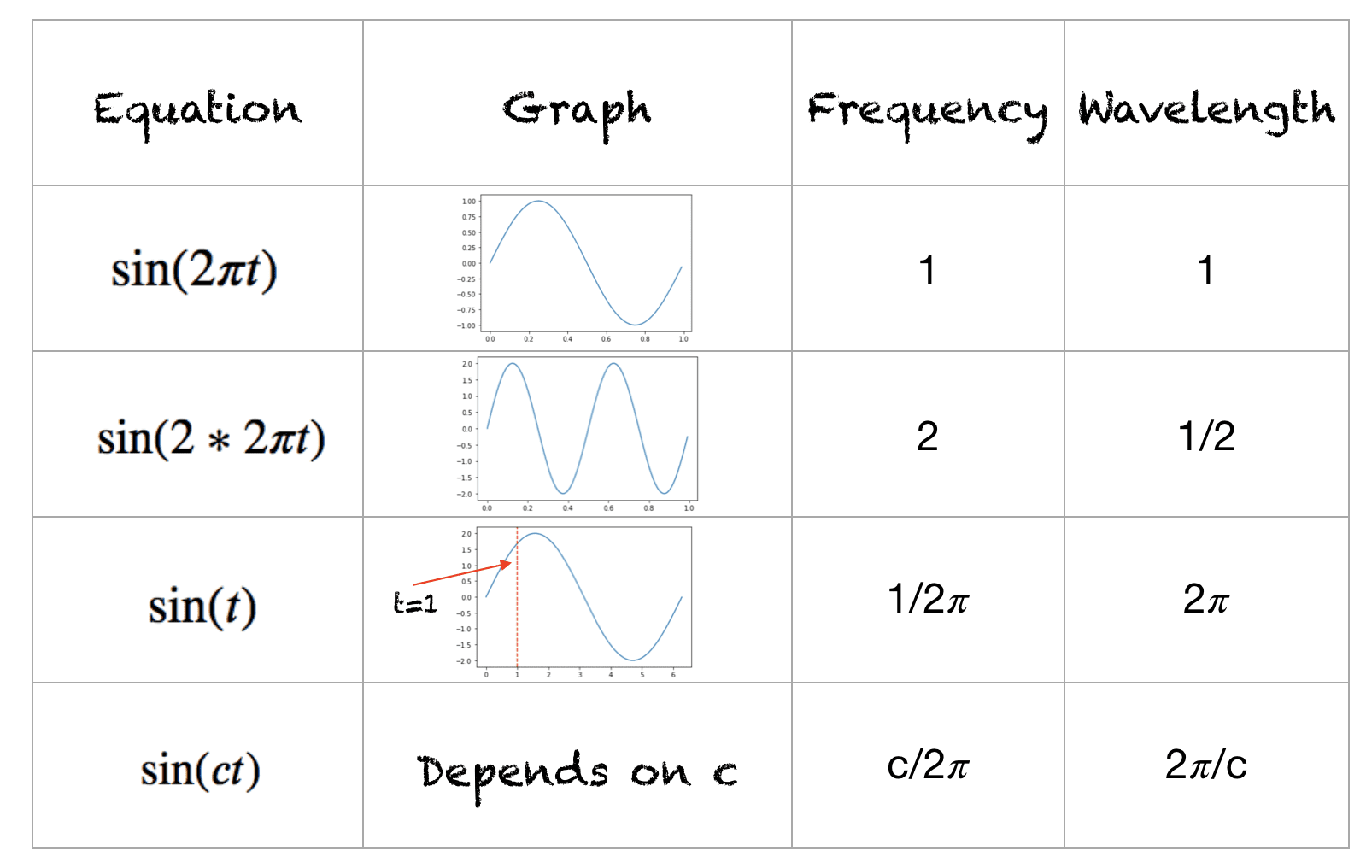
在物理中的正弦波中，波形的频率表示每秒内完成的周期数，而波长表示波形重复的距离。下图展示了不同波形的波长和频率。

PE2

正弦函数的波长

正弦函数的波长（wavelength）是指正弦波完成一个完整周期所需要的距离或时间。在公式上，正弦函数通常表示为：

\[y = \sin(kx + \phi) \tag{1}\]

其中：

  • $y$ 是输出值。
  • $x$ 是输入变量，通常代表时间或空间。
  • $k$ 是波数（wave number），它与波长 $\lambda$ 的关系是 $k = \frac{2\pi}{\lambda}$。
  • $\phi$ 是相位偏移。

因此，波长 $\lambda$ 的计算公式为：

\[\lambda = \frac{2\pi}{k}\]

1.2 Sinusoidal 位置编码公式

下面进入主题，假设有一个长度为 $L$ 的输入序列，并且需要获取该序列中第 $i$ 个元素的位置。位置编码通过不同频率的正弦和余弦函数来表示：

\[P(k, 2i) = \sin\Big(\frac{k}{10000.0^{2i/d}}\Big) \\ P(k, 2i+1) = \cos\Big(\frac{k}{10000.0^{2i/d}}\Big)\]

上述公式称为三角函数式位置编码，一般也称为 Sinusoidal 位置编码。其中：

  • $k$：输入序列中元素的位置，即第几个 token，$0 <= k < L/2$；
  • $d_{\text{model}}$ ：输出嵌入空间的维度；
  • $P(i)$：用于将输入序列中位置 $k$ 映射到位置矩阵中 $(k,j)$ 索引的映射函数；
  • 10,000：用户定义的标量，设定为 10,000，如论文《Attention Is All You Need》作者所使用的值。
  • $i$：用于映射到列索引，范围为 $0 \leq i < \frac{d}{2}$，每个 $i$ 值都同时映射到正弦和余弦函数应正弦和余弦函数。

在上面的公式中，可以看到偶数位置使用正弦函数，而奇数位置使用余弦函数。并通过 sin 和cos 函数将位置编码的取值固定在了 $[-1, 1]$ 之前，但是为什么不直接用线性函数？而且这里面的 10000 是怎么想到的？谷歌在论文里面给出了解释：

  1. 具有相对位置表达能力：Sinusoidal 可以学习到相对位置，对于固定位置距离的 $k$，$PE(i+k)$ 可以表示成 $PE(i)$ 的线性函数。
  2. 两个位置向量的内积只和相对位置 $k$ 有关。
  3. Sinusoidal 编码具有对称性。
  4. 随着 $k$ 的增加，内积的结果会直接减少，即会存在远程衰减。

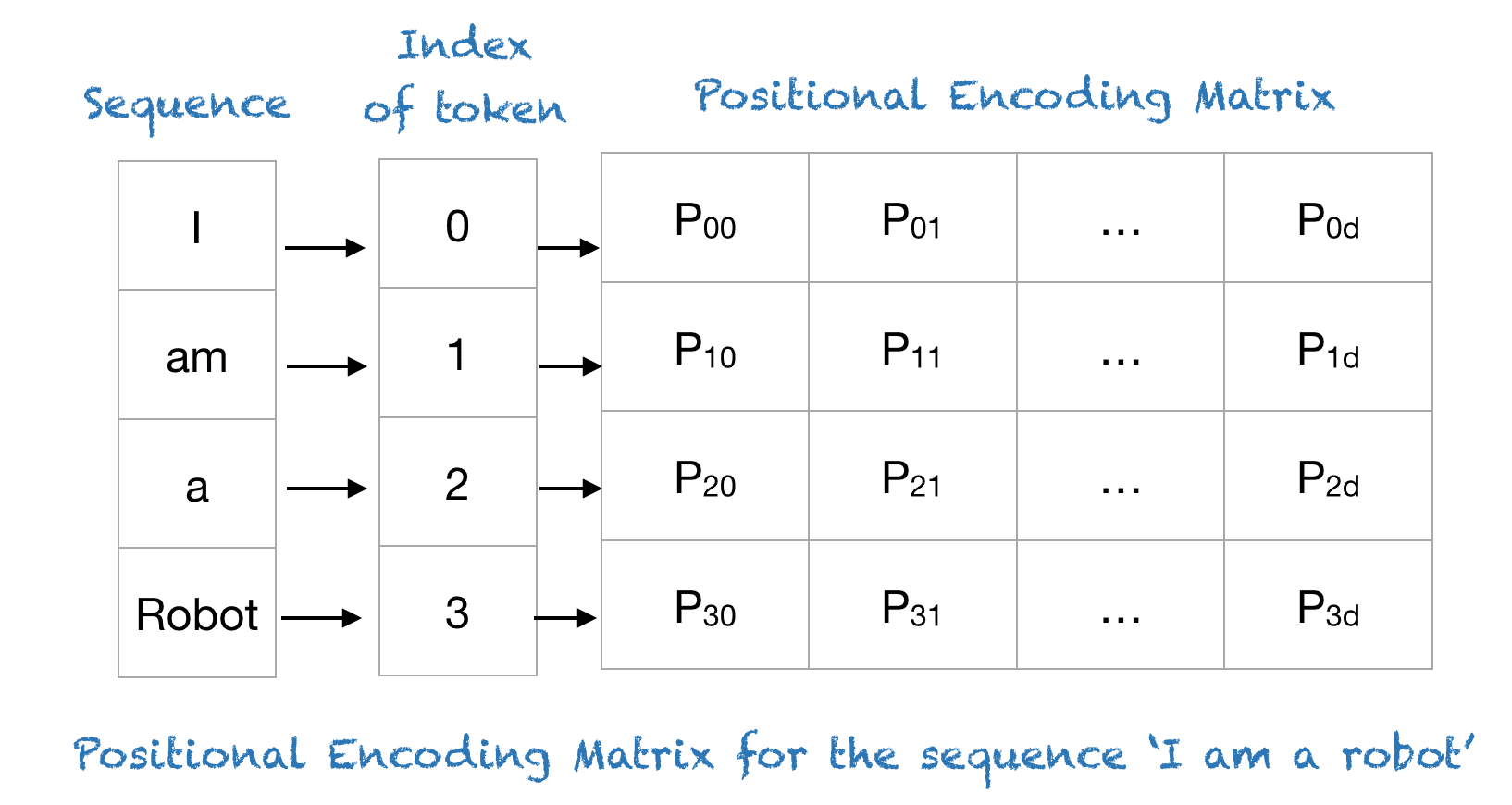
直接看公式不够直观，我们以短语“I am a robot”为例，其中 $n=100$ 且 $d=4$。下表展示了该短语的位置信息编码矩阵。实际上，对于任何由四个字符组成的短语，只要 n=100 且 d=4，其位置信息编码矩阵都相同。

PE_example

即，“I am a robot” 对应的位置编码矩阵如下所示:

array

二 Sinusoidal 位置编码实现及可视化

2.1 python 实现

下面是使用 NumPy 实现位置编码的简短 Python 代码。

import numpy as np
import matplotlib.pyplot as plt
 
def getPositionEncoding(seq_len, d, n=10000):
    P = np.zeros((seq_len, d))
    for k in range(seq_len):
        for i in np.arange(int(d/2)):
            denominator = np.power(n, 2*i/d)
            P[k, 2*i] = np.sin(k/denominator)
            P[k, 2*i+1] = np.cos(k/denominator)
    return P
 
P = getPositionEncoding(seq_len=4, d=4, n=100)
print(P)

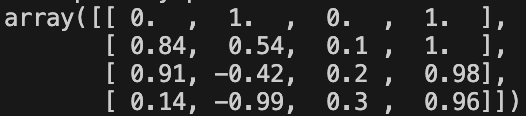
输出结果如下所示:

[[ 0.          1.          0.          1.        ]
 [ 0.84147098  0.54030231  0.09983342  0.99500417]
 [ 0.90929743 -0.41614684  0.19866933  0.98006658]
 [ 0.14112001 -0.9899925   0.29552021  0.95533649]]

2.2 理解位置编码矩阵

为了理解位置编码，我们首先来看一下 n=10,000 和 d=512 的不同位置的正弦波。

def plotSinusoid(k, d=512, n=10000):
    x = np.arange(0, 100, 1)
    denominator = np.power(n, 2*x/d)
    y = np.sin(k/denominator)
    plt.plot(x, y)
    plt.title('k = ' + str(k))
 
fig = plt.figure(figsize=(15, 4))    
for i in range(4):
    plt.subplot(141 + i)
    plotSinusoid(i*4)

PE 可视化如下所示:

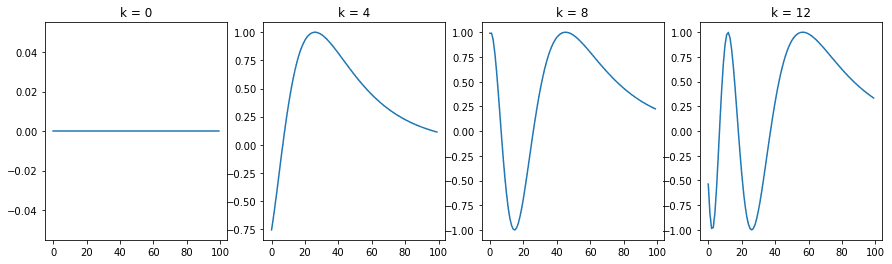
pe visual

可以看出，每个位置 $k$ 都对应一个不同的正弦波，它将该位置编码为一个向量。

结合前面的波长 $\lambda$ 的计算公式（1）和位置编码函数，可以确定，对于固定的嵌入维度 $i$，波长是通过以下公式确定的：

\[\lambda_{i} = 2 \pi n^{2i/d}\]

从公式可以看出，正弦波的波长随着嵌入维度 $i$ 的增长呈几何级数变化，波长从某个值到另一个值。因此，三角函数式位置编码方案有几个显著的优点：

  1. 正弦和余弦函数的取值范围在 $[-1, 1]$，保证了位置编码矩阵的值处于归一化范围内。
  2. 每个位置的正弦波不同，因此你可以用一种独特的方式来编码每个位置。
  3. 你可以衡量或量化不同位置之间的相似性，从而能够编码词语的相对位置。

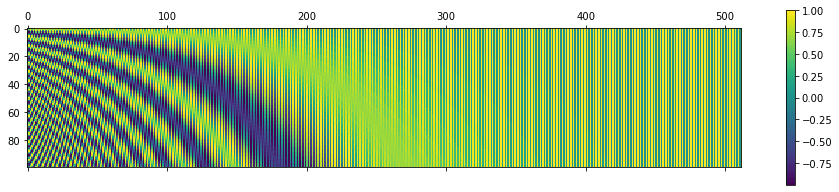
可以使用更大的数值来可视化位置矩阵。可以使用 Python 的 matplotlib 库中的 matshow() 方法。将 n=10,000 设置为与原论文一致时，你会得到如下图所示的结果：

# 调用 PE 函数生成一个 100 行、512 列的矩阵 P，表示 100 个位置的编码。
P = getPositionEncoding(seq_len=100, d=512, n=10000)
# 使用 matshow() 函数可视化位置编码矩阵 P。该函数生成矩阵的热力图，每个位置的编码值通过颜色的深浅来表示。
cax = plt.matshow(P)
# plt.gcf().colorbar(cax)：添加颜色条以显示数值和颜色之间的映射关系。
plt.gcf().colorbar(cax)

PE_matrix_visual

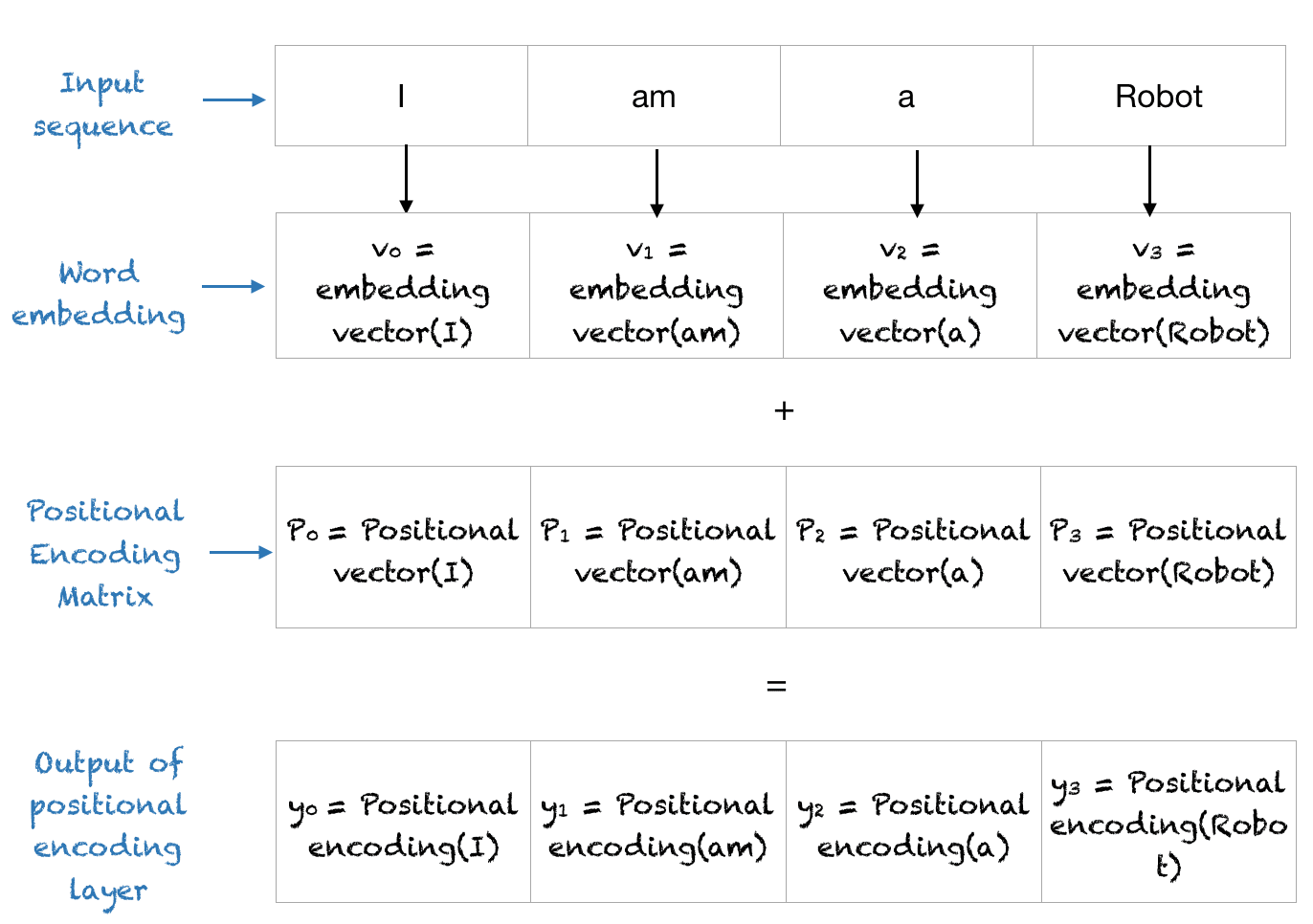
位置编码层的输出-位置向量与词嵌入向量相加，并将这个结果矩阵作为输入提供给后续层。整个过程如下图所示。

embedding workflow

Sinusoidal 位置编码深入理解

这篇文章给出了正弦编码的一些特性的推导，本文不再描述。下面是一些正弦编码（Sinusoidal）的特性总结：

1，相对位置表达能力

Sinusoidal 位置编码具备相对位置表达能力，即对于固定位置距离的 $k$，$PE(i+k)$ 可以表示成 $PE(i)$ 的线性函数。

2，对称性

Attention 中的内积结果只和相对位置 $k$ 有关，公式推导可得：

\[PE(t + k)PE(t) = \sum_{i=0}^{d/2-1}cos(k*w_{2i}),\; w_{2i} = 10000^{2i/d} \\ PE(t+k)PE(t) = PE(t)PE(t-k)\]

即 Sinusoidal 编码具有对称性。

3，远程衰减

随着 $k$ 的增加，位置向量的内积结果会逐渐降低，即会存在远程衰减。 如下图所示： PE7

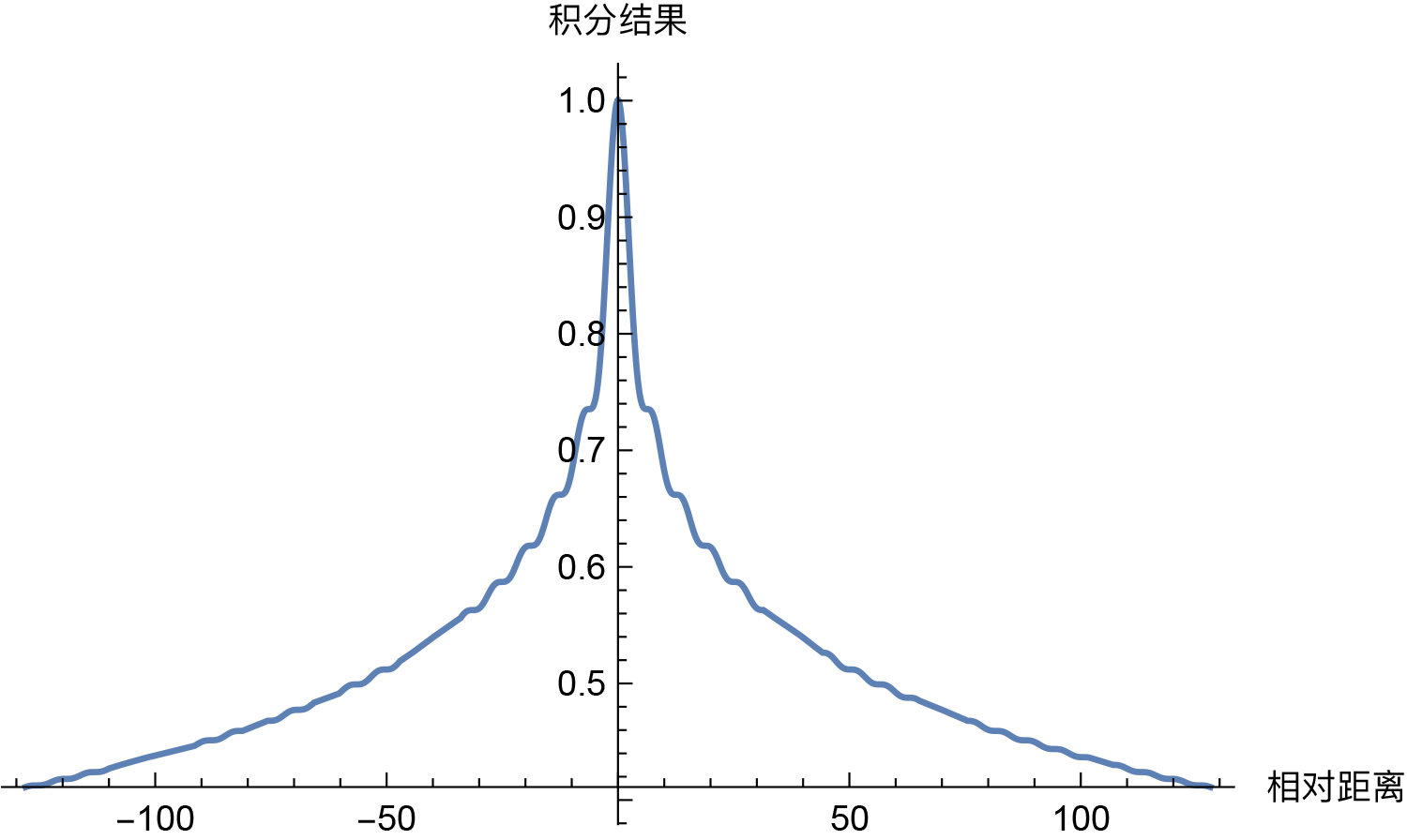
相对位置：第 n 个 token 与第 m 个 token 的位置差是 n−m。

4，为什么选择参数 base=10000

选择sin，cos是因为可以表达相对位置，以及具备远程衰减。但是sin/cos里面的参数10000是如何来的？

可以从 sin/cos 的周期性角度进行分析。分析周期可以发现，维度 i 的周期为 $T = base^{i/d}*2pi$，其中0 <= i < d，因此周期T的范围是 $T\in [2\pi, base * 2\pi]$。

固定 $d$ 为 100，维度 $i=10$，绘制不同 base 下的 position embedding，如下图所示:

PE7

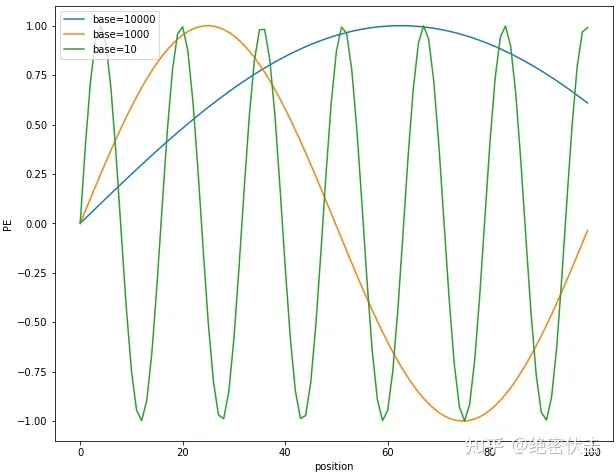
可以看到随着 base 的变大，周期会明显变长。Transformer 选择比较大的 base=10000，可能是为了能更好的区分不同位置 token 的 PE 值，防止其在不同位置有大量重复。

那为什么周期大能更好区分位置？

从上图可以看出，base 越大，周期越大。而周期越大，在 position 从 0~100 范围内，只覆盖了不到半个周期，这使得重复值少；而周期小的，覆盖了多个周期，就导致不同位置有大量重复的值。

Sinusoidal 编码是否真的具备外推性

那么还有最后一个问题，正弦编码是否真的具备外推性？

所谓外推性是指在长文本表征过程中，如何在训练阶段只需要学习有限的长度，即可以在推理阶段能够延伸长度至若干倍且依然保持不错的性能和效果。

上下文长度外推性其实是一个训练和预测的长度不一致的问题，主要体现在两个方面：

  1. 预测的时候用到了没训练过的位置编码（不论是绝对位置还是相对位置）；
  2. 预测的时候注意力机制所处理的 token 数量远超训练时的数量。

因为 Sinusoidal 位置编码中的正弦余弦函数具备周期性，并且具备远程衰减的特性，所以理论上也具备一定长度外推的能力，但是实际实验中它的外推性表现一般，在具备超长文本聊天的模型中，都没有使用 Sinusoidal 位置编码。

参考资料

你觉得有收获吗？❤️
Read More

位置编码算法背景知识

【2024-10-22】理解 RoPE 位置编码算法的原理和推导公式之前得先具备一些背景知识，主要是关于三角函数、旋转矩阵、直角坐标系、欧几里得内积的相关概念和公式，可以先快速阅览本章内容，后续关于 RoPE 算法的推导不理解的时候，再来细看相关公式和概念即可。