SmoothQuant 量化详解

Categories: LLM_Compression 2024-10-30

• 摘要
• 1. 介绍
• 2. 预备知识
• 3. 量化难点总结
• 4. SmoothQuant 算法
  • 4.1 SmoothQuant 算法实现及简单实验
• 5. 实验
  • 5.1 实验设置
  • 5.2 量化后精度对比实验
  • 5.3 加速和节省内存对比实验
  • 5.4 扩展：在单节点内运行 530B 模型
  • 5.5 消融研究
• 参考资料

先验知识：激活值是指模型中需要进行量化的计算密集层的输入，典型的就是线性层的输入，self-attention 层的输入等等。

摘要

SmoothQuant 是 PTQ（训练后量化）方案，量化位宽为 W8A8，即权重和激活都是用 8bit 量化，SmoothQuant 的核心贡献是，基于权重易量化而激活难量化的观察提出了一个解决办法：引入平滑因子 $s$ 来平滑激活中的异常值，并通过数学上的等效转换将量化的难度从激活迁移至权重上。这个方法可以使 INT8 量化能够应用于 LLMs 中所有的矩阵乘法运算。SmoothQuant 量化算法在保持模型精度不变的情况下，使得 LLMs 推理速度提升至 1.56 倍，内存需求减少至 50%。

1. 介绍

和 CNN 模型或较小的 Transformer 模型（如 BERT，Devlin 等，2019）不同，大型语言模型 (LLMs) 的激活非常难以量化。因为，将 LLMs 扩展至超过 67B 参数时，激活中会出现具有大幅度的系统性异常值 (Dettmers 等，2022)，导致较大的量化误差和准确性下降。这些离群值(outier)与正常值相比会有数百倍的数值差距。如果直接进行量化，会导致大部分数值清零，产生很大的精度损失。但同时又有研究表明，这部分离群值会对模型的性能产生显著影响，因此必须想办法保留离群值而不是直接清零，这就产生了一个难以调和的矛盾。

Outliers 是指激活中的 Outliers，权重的整体变化幅度还是比较小的。Outliers 的出现会使得量化更难进行，因为原始权重数值的变化范围变大了，而量化编码的精度是有限的，如 INT4 就只有 16 个数，这会导致了更大的量化误差。

ZeroQuant 和 LLM.int8() 提出了各自的解决办法：

1. ZeroQuant (Yao 等，2022) 应用了动态逐 token 激活量化和分组权重量化（定义见图 3 第 2 节）来解决激活离群值(outier)问题。虽然该方法实现效率较高，且对 GPT-3-350M 和 GPT-J-6B 提供了良好的准确性，但对于 175B 参数的 OPT 模型的准确性较差。
2. LLM.int8() (Dettmers 等，2022) 通过引入混合精度分解（即对异常值保持 FP16，其他激活使用 INT8）解决了该准确性问题，但是这种方法在工程上很难在 AI 加速器上高效实现，是一种硬件不友好的量化方案。

因此，寻找一种高效、对硬件友好且无需训练的量化方案，使得 LLMs 中所有计算密集型操作均采用 INT8，仍然是一个未解决的难题。由此，论文提出了 SmoothQuant 量化方案，和过去相比，SmoothQuant 是高效且准确的 PTQ 方案。SmoothQuant 的提出是基于一个关键观察：之所以激活比权重更难量化是因为其存在离群值(Dettmers et al., 2022), 不同 tokens 在其通道上表现出类似的变化。基于这一现象，SmoothQuant 离线地将量化难度从激活迁移至权重（如下图图 2 所示），并提出了逐通道的等效缩放转换，使跨通道的数值更为平滑，从而显著提升模型的量化友好性。

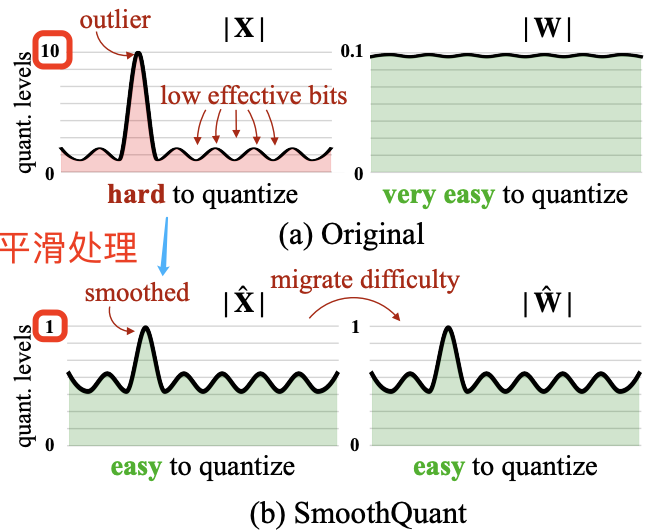
SmoothQuant 的核心思路是：激活 $X$ 之所以难以量化，是因为存在离群值拉伸了量化的线性映射范围，导致大部分数值的有效位数减少。我们在离线阶段将激活中的尺度变化转移到权重 $W$ 上，从而降低激活的量化难度。经过平滑处理的激活 $\hat{X}$ 和调整后的权重 $\hat{W}$ 均易于量化。

到这里可以看出 SmoothQuant 算法有两个难点：如何通过数学上的等效转换将量化的难度从激活迁移至权重上，以及如何实现逐通道的等效缩放转换。

2. 预备知识

1，量化公式：

在描述 SmoothQuant 的算法过程之前，得先掌握了解一些预备知识。量化是将高精度连续浮点数映射为低精度的离散整数，这里以经典的整数均匀量化（INT8）为例描述量化过程，量化公式如下所示：

其中 $X$ 是浮点张量，$X¯$ 是量化后的整数张量，$\Delta$ 是缩放系数，$\left\lfloor·\right\rceil$ 表示四舍五入函数，$N$ 为量化位数（此处为 8 位）。这里假设张量围绕 $0$ 对称；对于非对称情况（例如经过 ReLU 激活后的数据），可以通过添加零点来进行调整（Jacob 等，2018）。

该量化方法基于浮点数绝对值最大值来计算缩放系数 $\Delta$，这会保留激活中的异常值，而这些异常值对模型的准确性至关重要 (Dettmers 等，2022)。我们可以基于部分校准样本集的激活值离线计算缩放系数 $\Delta$，称为静态量化；也可以在模型运行时根据激活统计数据来动态计算缩放系数，称为动态量化。

2，量化粒度

所谓量化有不同的粒度其实是指基于不同的粒度去计算量化缩放系数。

常见量化粒度的可视化如图 3 所示，其中逐张量量化是整个矩阵共用一个缩放系数 $\Delta$，而逐 token 量化和逐通道量化则为每个 token 或权重的输出通道设定不同的缩放系数。逐通道量化的粗略形式是分组量化，即通道组之间使用不同缩放系数 (Shen 等，2020；Yao 等，2022)。

论文用 setp size 表示 $\Delta$，这不易理解，所以本文中描述为缩放系数。

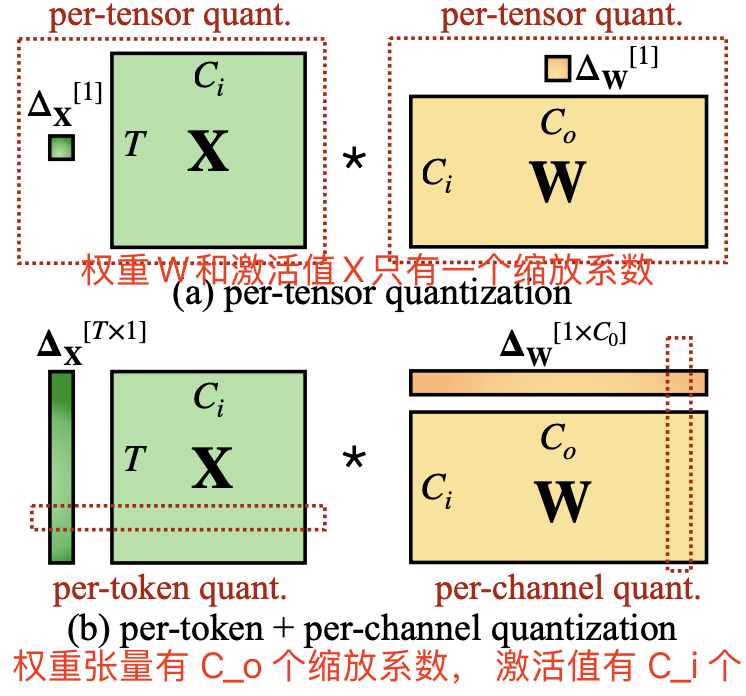
其中逐张量量化实现最简单、效率最高。为了在向量级量化中充分利用 INT8 GEMM 内核，我们只能在外部维度（如 token 维度 T 和输出通道维度 Co）上应用缩放因子，而无法在内部维度（如输入通道维度 Ci）上应用。

3，transformer 模型中的线性层。

Transformer(Vaswani 等，2017) 中的线性层计算公式如下所示：

其中 $T$ 表示 token 数，$C_i$ 为输入通道数，$C_o$ 为输出通道数（为简化省略批量维度，见图 3）。通过将权重量化为 INT8，可将存储需求减半。然而，为了加速推理，我们需要同时将权重和激活量化为 INT8（即 W8A8）以充分利用支持整数运算的内核（例如 INT8 GEMM），这些内核广泛支持于多种硬件（例如 NVIDIA GPUs、Intel CPUs、Qualcomm DSPs 等）。

很明显这里 Transformer 线性层中的通道数其实就是隐藏层大小，即 $C_i = C_o = \mathrm{hidden_ size}$。之所以用逐通道的概念，我猜是为了对应 CNN 模型中的张量通道概念，反正一般都是张量的最后一个维度。

3. 量化难点总结

1，激活比权重更难量化。

权重分布较均匀，易于量化。有研究表明 LLMs 的权重量化到 INT8 甚至 INT4 并不会影响精度 (Dettmers 等，2022；Yao 等，2022；Zeng 等，2022)，这与本论文的观察一致。

2，激活值中的离群值是导致大模型难以量化的重要因素。

激活中的离群值幅度比其他激活值大约 100 倍。对于逐张量量化（公式 1），异常值主导了最大幅度测量，从而压缩了非异常通道的有效量化位数（图 2）：假设某通道 $i$ 的最大幅度为 $m_i$，而整个矩阵的最大值为 $m$，则该通道的有效量化级别为 $2^8\cdot m_{i}/m$。对于非异常通道，有效量化级别会非常小（仅有 2-3 个级别），从而导致较大的量化误差。

3，离群值通常出现于特定通道。

作者对激活值进行了统计分析，发现离群值主要集中在少数通道中，一旦某个通道出现异常值，它会在所有 tokens 中持续存在（见图 4 红色标记）。对于特定 token，不同通道的激活值差异很大（少部分通道激活值很大，大部分通道较小），但同一通道内不同 tokens 的激活值幅度差异小（异常值通道幅度持续较大）。

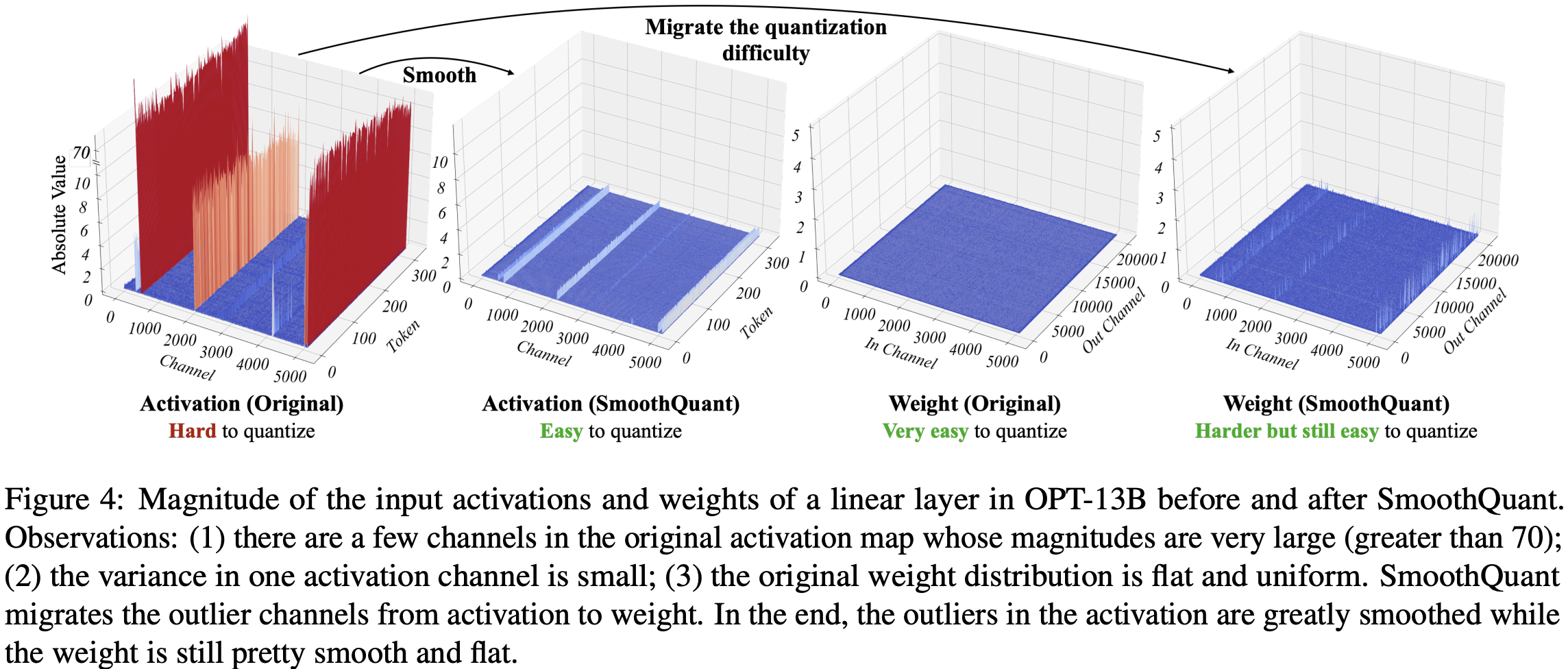
上述现象总结起来就是，离群值跟通道相关跟 token 无关，由此很明显，应该对激活采用逐通道量化 (Bondarenko 等，2021)（即每个通道使用不同的量化系数），这可以大幅降低量化误差，逐 token 量化则帮助不大。表 1 验证了这一假设：模拟的逐通道激活量化能使精度接近 FP16，与 Bondarenko 等的发现一致。

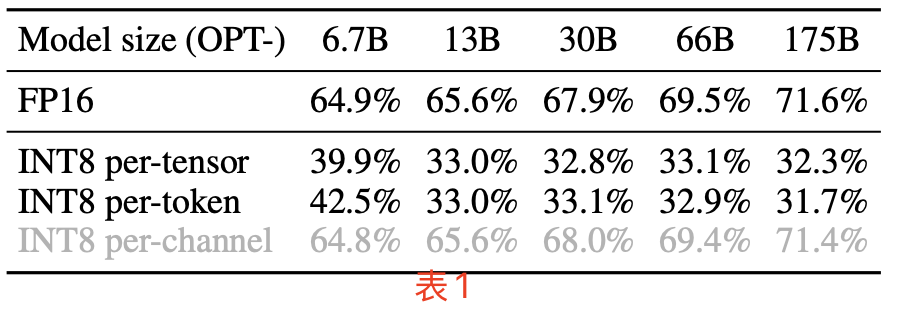
但是，逐通道激活量化并不适合硬件加速的 GEMM 内核（线性层计算），因为这些内核依赖于高吞吐量的连续操作（如 Tensor Core MMAs），无法容忍低吞吐量指令（如转换或 CUDA Core FMAs）的插入，而量化公式中无论是量化系数还是浮点数到定点数的转换都是用 CUDA Core 计算单元。

因此，在 GEMM 内核中，为了不降低 GEMM 内核本身的吞吐量，量化的缩放操作只能沿矩阵乘法的外部维度进行（即激活的 token 维度和权重的输出通道维度 $C_o$，见图 3），通常在矩阵乘法完成后应用：

因此，尽管逐 token 激活量化精度只比逐张量量化稍高一点，但是为了不降低GEMM 内核本身的吞吐量，过往的研究依然还是在线性层中采用了它(Dettmers 等，2022；Yao 等，2022)。

CUDA Core：用于执行传统的单一指令流任务，比如 FMA、加法、乘法等操作。每个 CUDA Core 每次只能执行一个简单的操作（如乘法和加法）。 Tensor Core：专门设计用于深度学习中的矩阵运算，特别适用于加速矩阵乘法和积累（MMA）操作。能直接支持混合精度运算（例如 FP16 运算），可以在单个时钟周期内执行多次乘法和累加操作，非常适合深度学习中的卷积操作和矩阵乘法。

4. SmoothQuant 算法

作者引入了一个 smoothing factor 向量，对激活值按通道除以 smoothing factor，从而降低激活值整体的方差。为了保持线性层在数学上的等价性，以相反的方式对权重进行对应调整：

简简单单的公式（3）就完成了对激活值中含有”离群值“的通道进行了平滑，把离群值“转移”到了权重上，这就是前面描述的将激活量化难度前移到权重上的原理，公式就一行，果然大道至简。

考虑到输入 $X$ 通常由前面的线性操作（如线性层、层归一化等）产生，我们可以轻松地将平滑因子离线地融合到前一层的参数中，不会因额外的缩放操作而导致增加内核调用开销。在一些其他情况下，例如当输入来自残差相加时，我们可以在残差分支中添加额外的缩放，类似于 Wei 等 (2022) 的方法。

1，将激活的量化难度迁移到权重上。

选择合适的逐通道的平滑因子 $s$，使得迁移后的激活 $\hat{X} = X \cdot \text{diag}(s)^{-1}$ 更易于量化，这个很关键也很难（后续的AWQ 量化算法就是改进了 $s$ 的计算策略）。那么如何选择合适的 smoothing factor 向量 $s$ 呢：

• 一种极端情况，是令 $s_j = \max(\vert\mathbf{X}_j\vert), \quad j = 1, 2, \dots, C_i$，这会使得激活值的离群值全部转移到权重上面，激活值变得很好量化，权重反而难以量化。
• 另一种极端情况，是令 $s_j = \frac{1}{\max(\vert\mathbf{W}_j\vert)}$，即将所有量化难度从权重迁移到激活，这会使得原本方差较小的权重方差更小，激活值方差更大。

因此，作者通过引入一个超参数 $\alpha$，来平衡这两种极端情况，如以下公式：

对于大多数模型，$\alpha = 0.5$ 是一个理想的平衡点，能够均匀分配量化难度，尤其是在对权重和激活使用相同量化器时（如逐张量、静态量化），公式（4）确保权重和激活的相应通道具有相似的最大值，从而共享相同的量化难度。图 5 展示了当 $\alpha = 0.5$ 时的平滑变换过程。

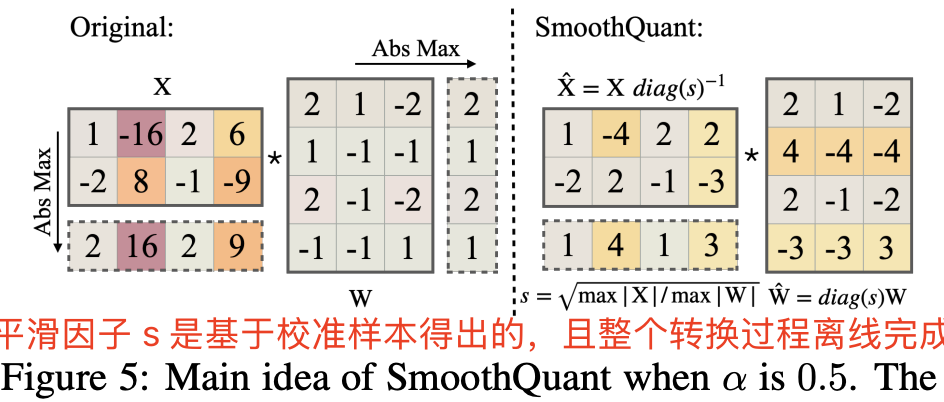
合适的迁移强度 $\alpha$（最佳平衡点）能够让激活和权重都便于量化。若 $\alpha$ 过大，权重的量化会变得困难；而若 $\alpha$ 过小，激活的量化会受到影响。对于一些激活异常值更显著的模型（如 GLM-130B (Zeng 等，2022)，其异常值约占 30%，使激活量化更具挑战），可以选择更大的 $\alpha$ 值，例如 0.75，以将更多量化难度迁移至权重。

2, 将 SmoothQuant 应用于 Transformer 模型中。

线性层占据了大型语言模型中大部分的参数量和计算开销。默认情况下，我们对自注意力和前馈层的输入激活进行平滑处理，并将所有线性层量化为 W8A8。同时，我们对注意力机制中的 BMM 操作进行量化。图 6 展示了我们针对 Transformer 模块设计的量化流程：对于计算密集的操作（如线性层和注意力层中的 BMM），我们将其输入和权重量化为 INT8，而对于 ReLU、Softmax、LayerNorm 等轻量级元素操作，则保持激活为 FP16。这样的设计使我们在准确性和推理效率间达到了良好的平衡。

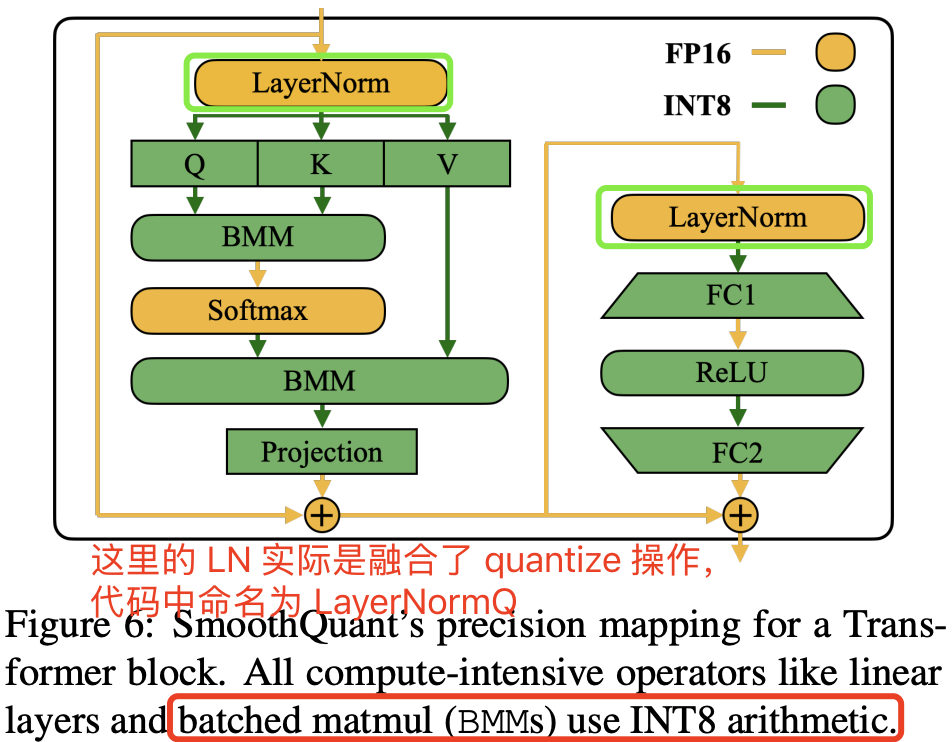
4.1 SmoothQuant 算法实现及简单实验

下述代码模仿官方仓库的量化算法，简单实现了对激活值、权重参数值进行了统计分析并可视化，以及应用了 smoothquant 后的平滑激活和权重统计值的可视化。真实的模型量化算法比这更复杂，校准集也更大，本代码只是尝试对特定层的特定线性层权重应用 SmoothQuant 量化，优点是代码可直接运行，更容易快速阅读来了解 SmoothQuant 的计算逻辑，仅供参考。

import torch
import numpy as np
import matplotlib
# 使用更快的非交互式后端，适合批量渲染
matplotlib.use('Agg')
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from transformers import AutoModelForCausalLM, AutoTokenizer
import os
import plotly.graph_objects as go
import plotly.io as pio
pio.renderers.default = 'svg'

# 加载模型和分词器
def load_model_and_tokenizer(model_name, device):
    from transformers import AutoTokenizer, AutoModelForCausalLM
    
    tokenizer = AutoTokenizer.from_pretrained(model_name)
    if tokenizer.pad_token is None:
        tokenizer.pad_token = tokenizer.eos_token  # 设置 eos_token 为 pad_token
    
    model = AutoModelForCausalLM.from_pretrained(model_name, torch_dtype=torch.float16 if device.type == 'cuda' else torch.float32).to(device)
    model.eval()
    return model, tokenizer

# 运行推理并获取激活值和权重
@torch.no_grad()
def get_activations_and_weights(model, tokenizer, texts, layer_index=4, channel_indexs=200, device=None):
    inputs = tokenizer(texts, return_tensors="pt", padding=True, truncation=True).to(device)
    with torch.no_grad():
        outputs = model(**inputs, output_hidden_states=True)
    print("outputs.hidden_states shape is ", len(outputs.hidden_states))
    activation = outputs.hidden_states[layer_index].abs()[:, :, :]  # 激活值

    # 尝试兼容不同模型结构
    try:
        layers = model.model.layers
    except AttributeError:
        try:
            layers = model.transformer.h
        except AttributeError:
            raise RuntimeError("无法自动识别 transformer 层结构，请手动指定。")
        
    q_weight = layers[layer_index].self_attn.q_proj.weight.abs()[:, :]
    k_weight = layers[layer_index].self_attn.k_proj.weight.abs()[:, :]
    v_weight = layers[layer_index].self_attn.v_proj.weight.abs()[:, :]
    weights = [q_weight, k_weight, v_weight]
    print(f"activation shape is {activation.shape} self_attn.q_proj.weight shape is {weights[0].shape}")
    return activation, weights

# 计算 SmoothQuant 的缩放因子
@torch.no_grad()
def calculate_scales(activation, fcs, alpha=0.5):
    original_shape = activation.shape
    act_reshaped = activation.view(-1, original_shape[-1]).abs().detach()
    device = activation.device
    act_max = torch.max(act_reshaped, dim=0)[0].float().to(device)
    weight_max_list = torch.cat([fc.abs().max(dim=0, keepdim=True)[0] for fc in fcs], dim=0)
    w_max = weight_max_list.max(dim=0)[0].clamp(min=1e-5).to(device)
    print(f"act_max shape is {act_max.shape}, w_max shape is {w_max.shape}")
    scales = act_max.pow(alpha) / w_max.pow(1 - alpha)
    print(f"scales shape is {scales.shape}")
    return scales

# 应用 SmoothQuant 缩放因子到激活值和权重
@torch.no_grad()
def apply_smoothquant_scaling(activation, weights, scales):
    smooth_activation = activation / scales.view(1, 1, -1)
    q_proj_weight = weights[0]
    smooth_q_weight = q_proj_weight * scales.view(1, -1)
    print(f"smooth_activation_sample shape is {smooth_activation.shape} q_proj smooth_weight shape is {smooth_q_weight.shape}")
    return smooth_activation, smooth_q_weight

# 检测离群值并打印通道索引
def find_outlier_channels(act, threshold=10):
    # 对每一列判断是否有元素 > threshold，得到布尔 mask，形状 [C]
    col_mask = (act > threshold).any(dim=0)

    # 提取列索引
    idx = torch.where(col_mask)[0]
    print("存在元素 >20 的通道索引:", idx.tolist())

# 3D 绘图函数
def plot_3d_plotly(data, title, html_file):
    """使用 plotly 画 3D Surface，并保存为 html。data 应为 numpy 2D。"""
    fig = go.Figure(data=[go.Surface(z=data.astype(np.float32))])
    fig.update_layout(title=title, autosize=True,
                      scene=dict(xaxis_title='Channel', yaxis_title='Token', zaxis_title='Absolute Value'))
    fig.write_html(html_file)
    print(f"已保存图表 {html_file}")

# 主函数，执行各个步骤
def main():
    model_name = "/llm_weights/Qwen3-1.7B"
    layer_index=2
    device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
    try:
        model, tokenizer = load_model_and_tokenizer(model_name, device)
    except Exception as e:
        print(f"模型加载失败: {e}")
        return
    input_texts = [
        "The quick brown fox jumps over the lazy dog. " * 2,
        "Artificial intelligence is revolutionizing the world. " * 2,
        "Large language models are powerful tools for NLP tasks. " * 2,
        "The meaning of life is to find " * 2
    ]

    activation_sample, weight_sample = get_activations_and_weights(model, tokenizer, input_texts, layer_index=layer_index, device=device)

    # 检查离群值所在通道
    find_outlier_channels(activation_sample)

    # 计算 SmoothQuant 缩放因子并应用平滑转换
    scales = calculate_scales(activation_sample, weight_sample)
    smooth_activation_sample, smooth_weight_sample = apply_smoothquant_scaling(activation_sample, weight_sample, scales)
 
    try:
        y_max = max(
            np.max(activation_sample.cpu().numpy()),
            np.max(smooth_activation_sample.cpu().numpy()),
            np.max(weight_sample[0].cpu().numpy()),
            np.max(smooth_weight_sample.cpu().numpy())
        )
        batch_size, seq_len, hidden_size = activation_sample.shape
        activation_sample_2d = activation_sample.view(-1, hidden_size)
        smooth_activation_sample_2d = smooth_activation_sample.view(-1, hidden_size)

        # 使用 plotly 绘图并保存 html
        plot_3d_plotly(activation_sample_2d.detach().cpu().numpy(),
                       f"Layer {layer_index} Activation (Original) - Hard to quantize",
                       "activation_original.html")
        plot_3d_plotly(smooth_activation_sample_2d.detach().cpu().numpy(),
                       f"Layer {layer_index} Activation (SmoothQuant) - Easy to quantize",
                       "activation_smooth.html")
        plot_3d_plotly(weight_sample[0].detach().cpu().numpy(),
                       f"Layer {layer_index} Weight (Original) - Very easy to quantize",
                       "weight_original.html")
        plot_3d_plotly(smooth_weight_sample.detach().cpu().numpy(),
                       f"Layer {layer_index} Weight (SmoothQuant) - Harder but still easy to quantize",
                       "weight_smooth.html")
        # 保存张量数据
        torch.save({
            'activation_original': activation_sample.cpu(),
            'activation_smooth': smooth_activation_sample.cpu()
        }, 'activation_tensors.pt')

        torch.save({
            'weight_original': weight_sample[0].cpu(),
            'weight_smooth': smooth_weight_sample.cpu()
        }, 'weight_tensors.pt')
        print("激活和权重张量已保存为 activation_tensors.pt 与 weight_tensors.pt")
    except Exception as e:
        print(f"绘图失败: {e}")
        return

if __name__ == "__main__":
    main()

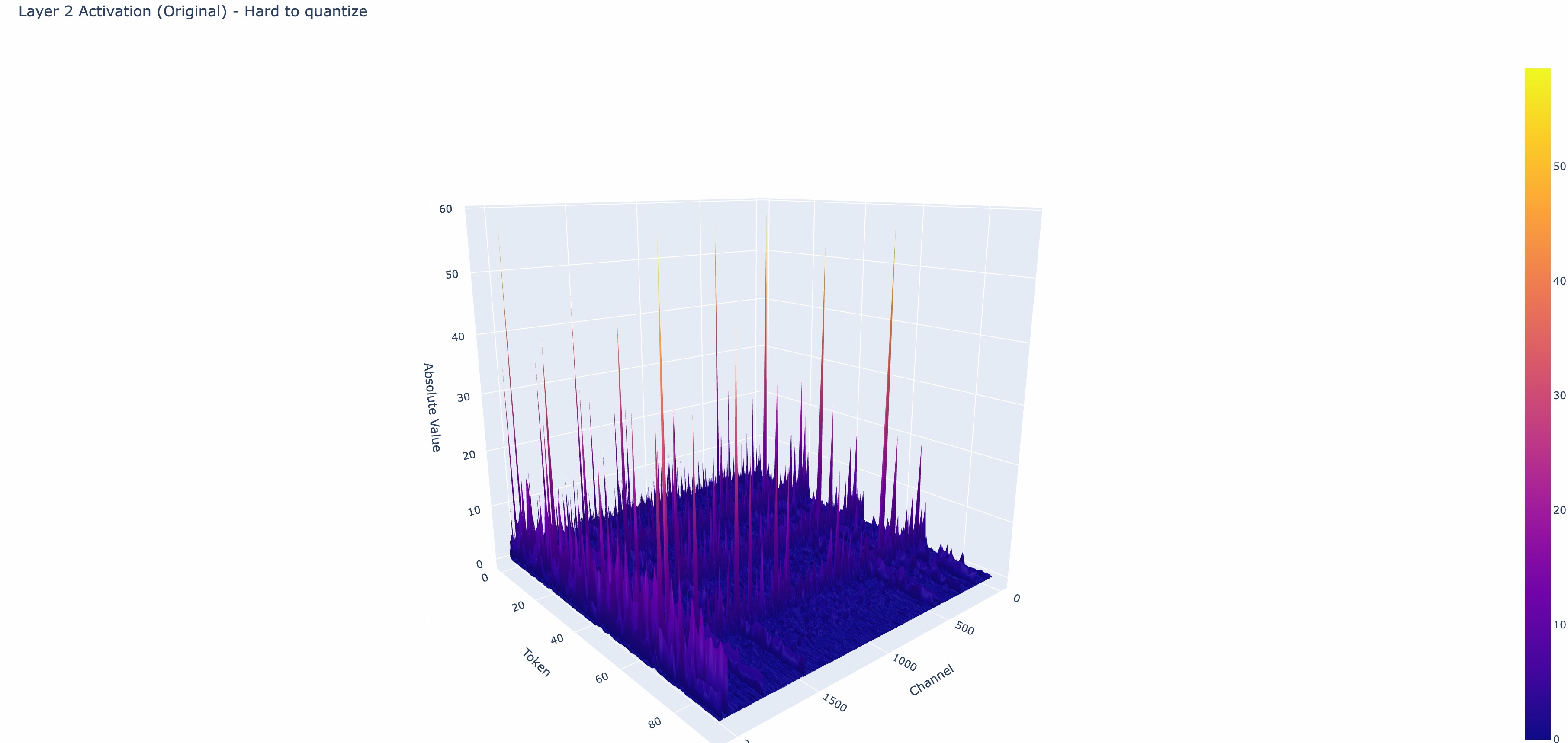
代码运行分别测试了好几个层的输入激活值和 q、k 线性层权重及其平滑后的可视化结果如下图所示，我的实验没有完全复现出了作者观察到的现象“离群值通常出现于特定通道”的那种完美现象，但是确实离群值会倾向在特定通道。

5. 实验

5.1 实验设置

作者在两个后端实现了 SmoothQuant：(1) PyTorch Huggingface，用于概念验证；(2) FasterTransformer，作为高性能生产环境框架的示例。

在 PyTorch Huggingface 和 FasterTransformer 框架中，作者基于 CUTLASS INT8 GEMM 内核实现了 INT8 线性模块和批量矩阵乘法 (BMM) 功能，并直接将原先的浮点（FP16）线性模块和 BMM 函数替换为 INT8 内核，从而构建 INT8 模型推理。

5.2 量化后精度对比实验

作者做了大量的实验证明了，SmoothQuant 在不同类型、不同规模的 LLM 上，都能 INT8 量化下保持与 FP16 相当的精度。即使是最新的 Llama-2 (Touvron 等，2023b)、Falcon (Almazrouei 等，2023)、Mistral (Jiang 等，2023) 和 Mixtral (Jiang 等，2024) 模型，也能实现无损的 W8A8 量化，如下表 7 所示:

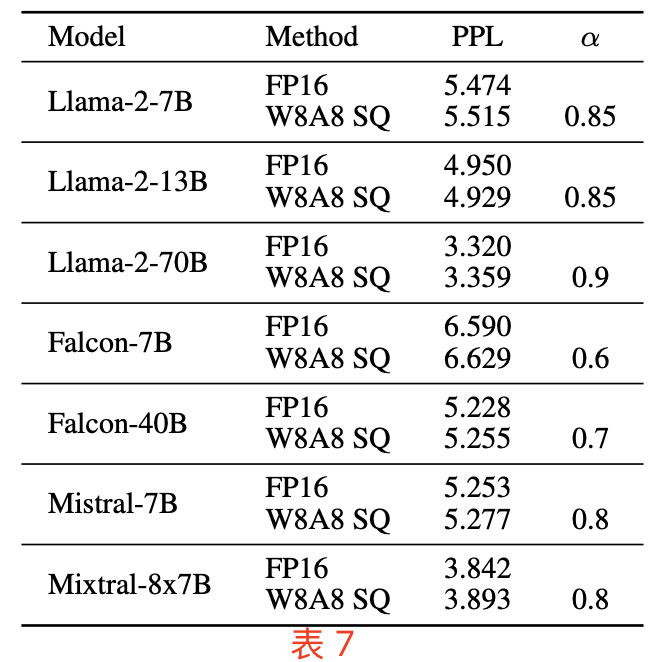
SmoothQuant 中使用逐 token 激活量化和逐通道权重量化。

5.3 加速和节省内存对比实验

本节中的实验展示了集成到 PyTorch 和 FasterTransformer 中的 SmoothQuant-O3 的实际加速和内存节省效果。

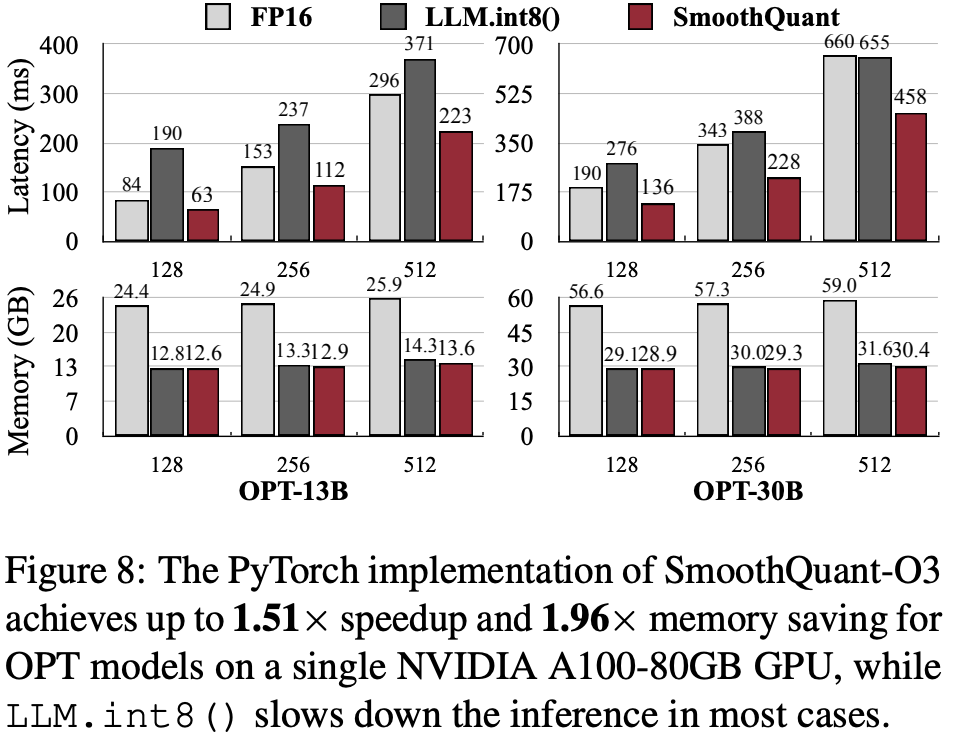
Prefill 阶段 PyTorch 实现。

图 8 展示了基于 PyTorch 实现的推理延迟和峰值内存使用情况。SmoothQuant 一直比 FP16 基线更快，在 OPT-30B 模型（序列长度为 256）上实现了 1.51 倍的加速。同时，观察到，模型越大，加速越显著。与之对比，LLM.int8() 几乎总是比 FP16 基线慢，因为它的混合精度激活表示产生了较大的开销。在内存使用上，SmoothQuant 和 LLM.int8() 都能将 FP16 模型的内存占用几乎减半；其中，SmoothQuant 节省的内存略多一些，因为它采用了全 INT8 GEMM 运算。

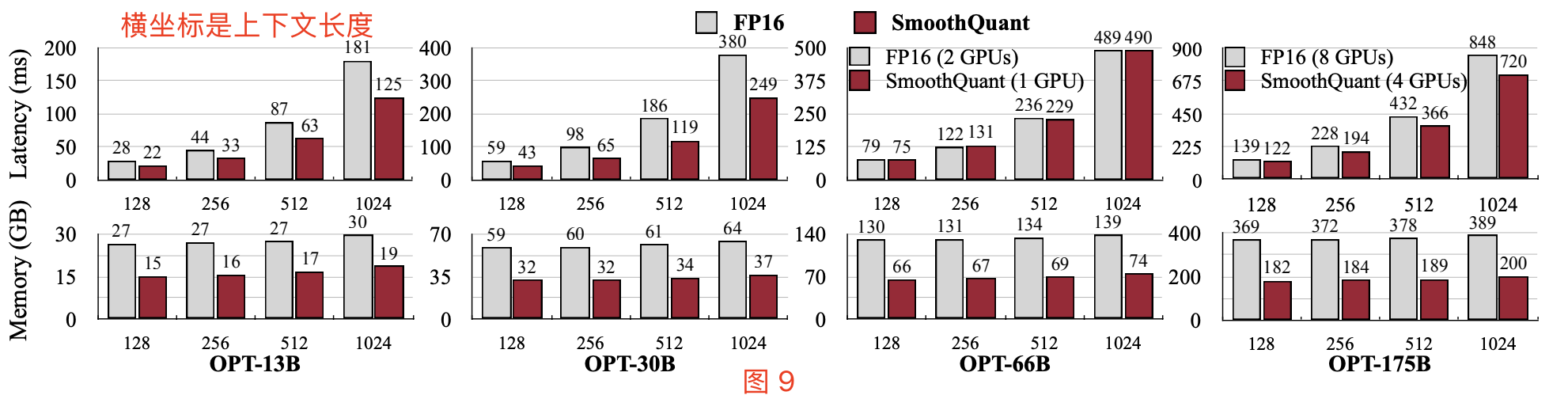
Prefill 阶段 FasterTransformer 实现

如图 9（顶部）所示，与 FasterTransformer 的 FP16 实现的 OPT 相比，单 GPU 情况下 SmoothQuant-O3 可以进一步减少 OPT-13B 和 OPT-30B 的执行延迟，最高可达 1.56 倍加速。值得一提的是，对于必须分布在多个 GPU 上的大型模型，SmoothQuant 在使用一半 GPU 数量的情况下实现了相似甚至更好的延迟表现。

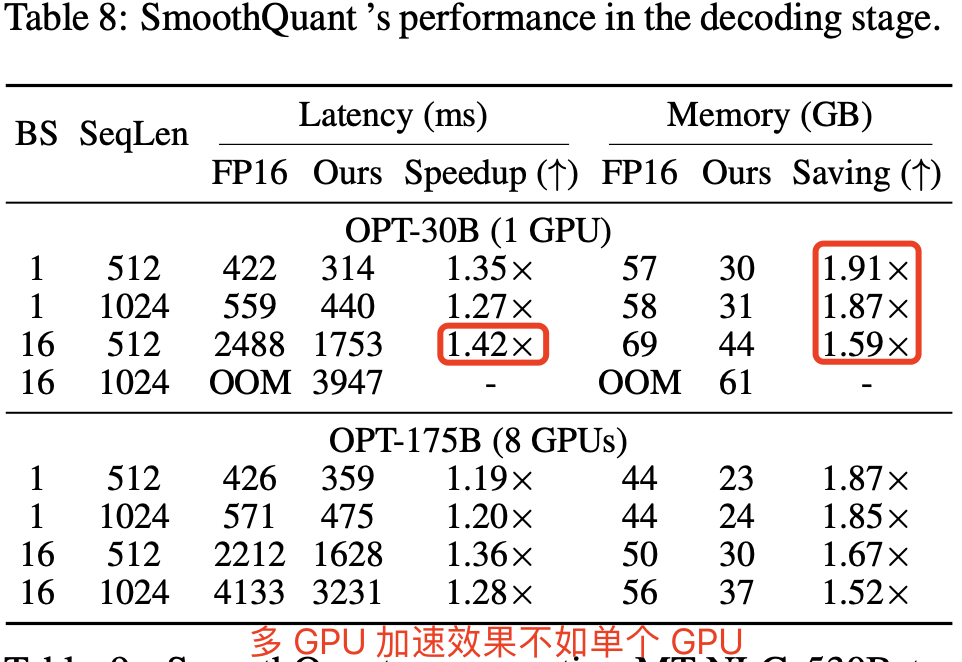
decode 阶段。

表 8 显示 SmoothQuant 可以大幅加速 LLM 的自回归解码阶段。相比 FP16，SmoothQuant 持续降低了逐 token 解码的延迟，最高达 1.42 倍加速。此外，SmoothQuant 将 LLM 推理的内存占用减半，使得部署成本大幅降低.

5.4 扩展：在单节点内运行 530B 模型

如表 9 和表 10 所示，SmoothQuant 能够在几乎无精度损失的情况下量化 530B 模型。模型尺寸的减小使得我们在相似的延迟下，仅需一半的 GPU 数量（从 16 减至 8）即可运行该模型，从而支持在单个节点（8×A100 80GB GPU）上部署超过 500B 的模型。

5.5 消融研究

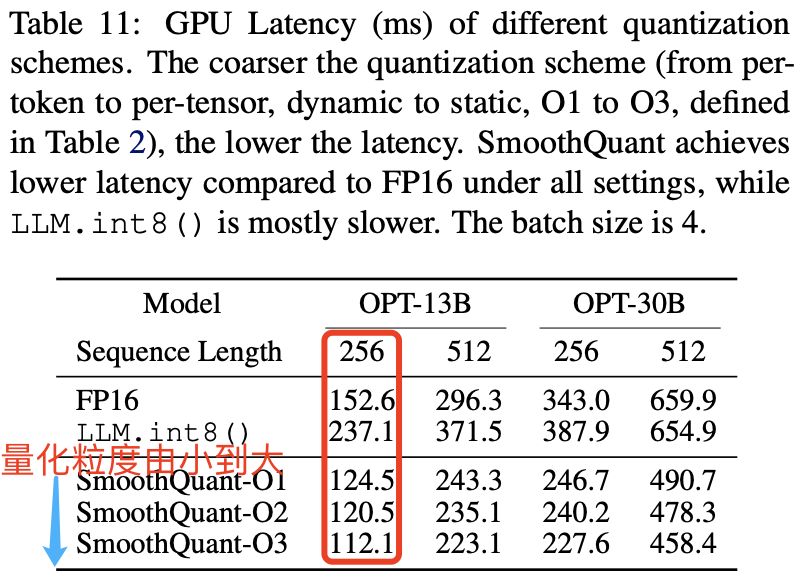
量化方案：量化粒度对延迟的影响。表 11 显示了基于我们 PyTorch 实现的不同量化方案的推理延迟。可以看到，量化粒度越粗（从 O1 到 O3），延迟越低。此外，静态量化可以显著加速推理，因为不再需要在运行时计算量化步长。在所有设置下，SmoothQuant 的速度都比 FP16 基线更快，而 LLM.int8() 通常较慢。如果精度允许，我们建议使用较粗的量化方案。

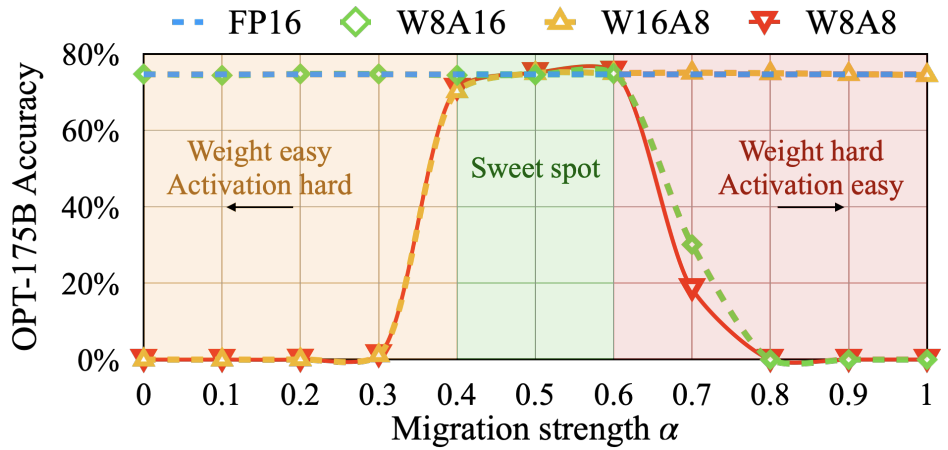
迁移强度：$\alpha$ 超参数对精度的影响。我们需要找到合适的迁移强度 $\alpha$（参见方程 4）来平衡权重和激活的量化难度。图 10 显示了在 OPT-175B 上使用 LAMBADA 测试不同 $\alpha$ 值的效果。当 $\alpha$ 过小（<0.4）时，激活难以量化；当 $\alpha$ 过大（>0.6）时，权重难以量化。只有在选择位于最佳平衡区间（0.4-0.6）的 $\alpha$ 时，才能同时减少权重和激活的量化误差，并在量化后保持模型性能。

参考资料

• 深入理解SmoothQuant量化技术
• SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models
• https://github.com/mit-han-lab/smoothquant