SmoothQuant 源码剖析
Categories: LLM_Compression
总结：smoothquant 从实现角度可拆开成两部分： 逐通道 smooth（平滑）权重和逐-token/逐 tensor 量化权重。
一 量化范围和粒度
1.1 量化范围
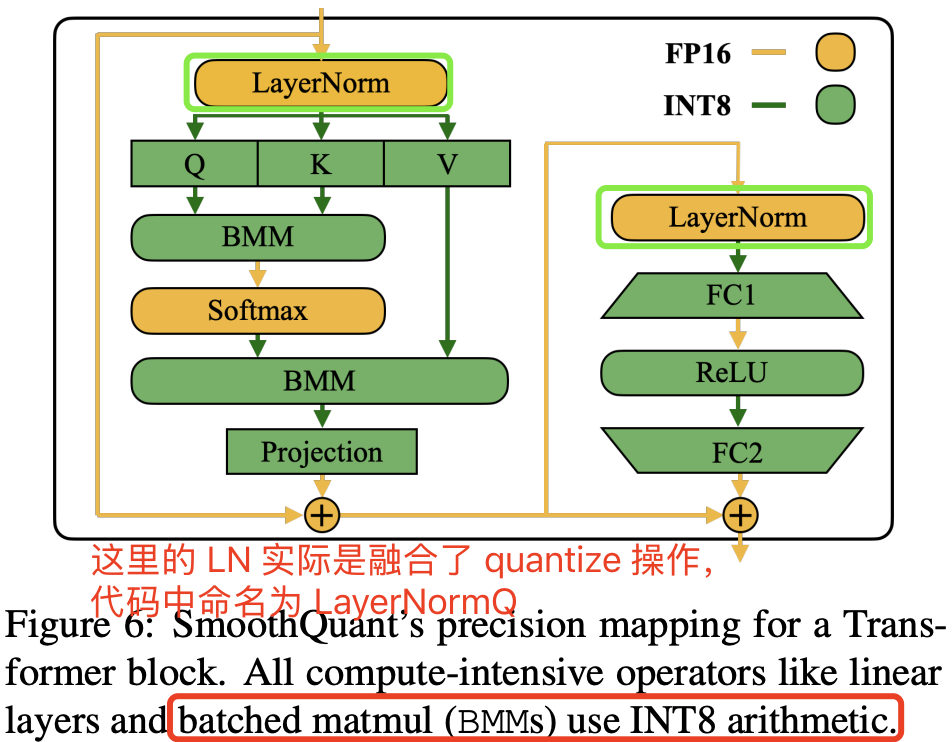
量化范围在论文中已经指出来了，decode layer 中的量化 layer 如下：
self-attention中的:q_liner、k_liner、v_linerout_linear、以及 $QK^T$ 对应的BMM（批量矩阵乘法），以及注意力输出线性层；mlp中的全部线性层以及激活层。
到这里我们会发现，transformer 中没有被量化的只有 Token Bmbedding 层、LayerNorm 层（llama 中是 RMSNorm 层），我个人推测之所以不量化 Token Bmbedding 层，是因为其参数冗余性较小且不存在权重稀疏现象，这个通过可视化 Token Bmbedding 层的权重值统计分布可以观测得到。
1.2 量化粒度
论文中提到 SmoothQuant 一共提供了 3 种量化量化粒度，从细到粗分别是：per-channel、per-token、per-tensor 量化，不同的粒度本质上是指基于不同的粒度去计算量化缩放系数。它们的定义描述如下:
per-tensor量化: 为整个张量使用一个统一的缩放系数（scale）和零点（zero point）;per-token量化：同一token（如序列中的每个单词或子词）才使用统一的缩放系数和零点，量化后缩放系数有[batch_size * seq_len]个；per-channel量化：同一embeeding维度的才使用相同的缩放系数和零点，缩放系数总共[hidden_size]个；对于 CNN 模型，则是为张量的每个通道（例如，卷积层的每个输出通道或线性层的每个输出特征）使用独立的缩放因子和零点。
权重 weight 支持per-channel、per-tensor 量化，其中获取权重张量最大值的区别如下所示：
import torch
import torch.nn as nn
fc1 = nn.Linear(512, 512,) # shape is [h, h]
w1 = fc1.weight
max1 = w1.abs().max() # 1, per-tensor compute max, max1 is a Scalar
max2 = w1.abs().max(dim=-1, keepdim=True)[0] # 2, per-channel computex, max2 shape is [h, ]
print(f"per-tensor max value is {max1}, per-channel max shape is {max2.shape}")
"""
per-tensor max value is 0.04419414699077606, per-channel max shape is torch.Size([512, 1])
"""
激活值 支持per-token、per-tensor 量化，其中获取权重张量最大值的区别如下所示：
input = torch.randn([16, 64, 512]) # input shape is [batch_size, seq_len, hidden_dim]
input.view(-1, input.shape[-1])
input_max1 = input.abs().max() # input_max1 is Scalar
input_max2 = input.abs().max(dim = -1, keepdim=True)[0] # input_max1 is [batch_size * seq_len, ]
print(f"activation per-tensor max value is {input_max1}, activation per-channel max shape is {input_max2.shape}")
"""
activation per-tensor max value is 4.675, activation per-channel max shape is torch.Size([16, 64, 1])
"""
很明显，激活基于 per-token 量化去算最大值，其输出维度就是 [batch_size, seq_len], 即保留 tokens 维度。这里假设输入是 2D 张量来分析 per-token 和 per-channel 计算的区别，重点在于理解沿着哪个维度做计算，示例代码如下所示：
>>> act
tensor([[4, 5, 5, 6, 6, 6, 6, 6, 8, 9],
[2, 2, 2, 2, 2, 7, 8, 3, 4, 2],
[4, 5, 6, 6, 7, 8, 1, 6, 8, 2]])
>>> max = torch.tensor([[2], [2], [2]])
>>> act /max
tensor([[2.0000, 2.5000, 2.5000, 3.0000, 3.0000, 3.0000, 3.0000, 3.0000, 4.0000,
4.5000],
[1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 3.5000, 4.0000, 1.5000, 2.0000,
1.0000],
[2.0000, 2.5000, 3.0000, 3.0000, 3.5000, 4.0000, 0.5000, 3.0000, 4.0000,
1.0000]])
>>> weight
tensor([[4, 5, 5, 6, 6, 6, 6, 6, 8, 9],
[2, 2, 2, 2, 2, 7, 8, 3, 4, 2],
[4, 5, 6, 6, 7, 8, 1, 6, 8, 2]])
>>> scale = torch.tensor([2,2,2,3,4,5,6,7,8,9])
>>> weight / scale
tensor([[2.0000, 2.5000, 2.5000, 2.0000, 1.5000, 1.2000, 1.0000, 0.8571, 1.0000,
1.0000],
[1.0000, 1.0000, 1.0000, 0.6667, 0.5000, 1.4000, 1.3333, 0.4286, 0.5000,
0.2222],
[2.0000, 2.5000, 3.0000, 2.0000, 1.7500, 1.6000, 0.1667, 0.8571, 1.0000,
0.2222]])
再结合前面的量化公式：
\[X¯_{\text{INT8}} = \left\lfloor \frac{X_{\text{FP16}}}{\Delta} \right\rceil, \quad \Delta = \frac{\max(|X|)}{2^{N-1} - 1} \tag{1}\]我们就可以实现权重和激活的量化算法，代码如下所示：
@torch.no_grad()
def quantize_weight_per_channel_absmax(weight, n_bits=8):
"""
按每个 token 的绝对最大值进行激活量化
参数:
- weight (torch.Tensor): 权重张量, shape is (hidden_size, hidden_size).
- n_bits (int): 量化位数, 默认 8
返回:
torch.Tensor: 量化后的激活张量
"""
weight_max = weight.abs().max(dim = 0, keepdim = True)[0] # 逐 token 计算最大值
q_max = pow(2, n_bits) - 1
scales = weight_max.clamp(min=1e-5) / q_max
quantized = (weight / scales).round().clamp(-q_max, q_max).to(torch.int8)
return quantized, scales
@torch.no_grad()
def quantize_activation_per_token_absmax(act, n_bits=8):
"""
按每个 token 的绝对最大值进行激活量化
参数:
- act (torch.Tensor): 激活张量, 本质上是线性层的输入张量, shape is (batch_size, seq_len, hidden_size).
- n_bits (int): 量化位数, 默认 8
返回:
torch.Tensor: 量化后的激活张量
"""
original_shape = act.shape
act_reshaped = act.view(-1, original_shape[-1]) # 重塑激活张量为 (batch_size * seq_len, hidden_size), 方便逐 token 量化
act_max = act.abs().max(dim = -1, keepdim = True)[0] # 逐 token 计算最大值
q_max = pow(2, n_bits) - 1
scales = act_max.clamp(min=1e-5) / q_max
quantized = (act_reshaped / scales).round().clamp(-q_max, q_max).to(torch.int8)
dequantized = quantized.float() * scales
dequantized = torch.view(original_shape)
return dequantized, scales
@torch.no_grad()
def quantize_activation_per_tensor_absmax(tensor, n_bits=8):
"""
按激活整个张量的绝对最大值进行激活量化
参数:
- act (torch.Tensor): 激活张量, 本质上是线性层的输入张量, shape is (batch_size, seq_len, hidden_size).
- n_bits (int): 量化位数, 默认 8
返回:
torch.Tensor: 量化后的激活张量
"""
scale = tensor.abs().max()
q_max = 2 ** (n_bits - 1) - 1 # 对于int8, q_max=127
scale = max(scale.item(), 1e-5) / q_max
quantized_tensor = (tensor / scale).round().clamp(-q_max, q_max).to(torch.int8)
return quantized_tensor, scale
def test():
# weight = torch.randn([32, 32])
weight = torch.tensor([[1.0, -2.0, 3.0, -4.0],
[5.0, -6.0, 7.0, -8.0]], dtype=torch.float32)
quant_w, scales = quantize_weight_per_channel_absmax(weight)
print(quant_w)
print(scales)
print(f"\nquant_w and scales shape is {quant_w.shape}, {scales.shape}")
if __name__ == "__main__":
test()
程序运行后输出结果如下所示:
tensor([[ 51, -85, 109, -127],
[ -1, 1, -1, 1]], dtype=torch.int8)
tensor([[0.0196, 0.0235, 0.0275, 0.0314]])
quant_w and scales shape is torch.Size([2, 4]), torch.Size([1, 4])
经测试 per-channel、per-token、per-tensor 量化函数均正确。
到这里，我们只是理解了三种量化方式的原理，以及实现过程，虽然这还是以前的量化知识，但这是理解 SmoothQuant 源码的先验知识。
二 SmoothQuant 项目剖析
2.1 SmoothQuant 代码概述
先快速看下整个项目的文件统计情况:
├── act_scales # 统计得到的激活值
│ ├── opt-13b.pt
│ └── ...
├── examples
│ ├── export_int8_model.py # realQunat -如何导出INT8模型
│ ├── generate_act_scales.py # common-统计激活值
│ ├── smoothquant_opt_demo.ipynb # fakeQunat -基于 torch 的伪量化
│ └── smoothquant_opt_real_int8_demo.ipynb # realQuant -torch+CUTLASS 量化的过程
├── figures # SQ量化方案与效果图
│ ├── accuracy.png
│ └── ...
├── LICENSE
├── README.md
├── setup.py
└── smoothquant
├── calibration.py # common - 通过校准集，统计得到 act_scales，其实是权重和激活的最大值用于计算 s
├── fake_quant.py # fakeQunat - 伪量化操作
├── __init__.py # 标识包目录
├── opt.py # realQunat - 量化 opt 模型
└── smooth.py # common - 模型平滑
量化算法实现在 smoothquant/smoothquant 目录中，它分别实现了基于 pytorch 的 FP32 计算 kernel 的伪量化推理，以及基于 CUTLASS 实现的 INT8 计算 kernel 的真量化模型推理，同时将量化过程分成三个模块，过程拆解和各自对应的文件如下所示:
- 根据校准集生成激活值 scales，实际是各
channel的最大值，实现在calibration.py。 - 使用激活值和权重的 scales（通道最大值）逐通道计算的平滑因子 $s$，并融合进线性层权重参数里面，从而实现将激活量化难度转移至权重的目的，实现在 smooth.py。
- 模型量化及量化模型推理。
- 伪量化模型推理（量化算法验证）: 模型权重量化实现是在
W8A8Linear().from_float(...)函数中，采用了经典的最大绝对值量化（对称量化），然后就是伪量化模型推理，实现在fake_quant.py。 - 真量化模型推理: 量化 kernel 和量化算法实现来源于作者的另外一个仓库-
torch_int，分别基于 CUTLASS 的 API 实现 Linear 和 BMM 的各种量化 kernel，实现在 torch_int/nn/linear.py，并有对称和非对称量化权重和激活的函数，实现在 torch_int/functional/quantization.py；使用from_float函数完成量化模型转换，并用量化 kernel 替换之前模型的 FP32 kernel，最后就是正常的模型推理过程，实现在opt.py。
- 伪量化模型推理（量化算法验证）: 模型权重量化实现是在
上述模块的功能验证在 example 目录中，比如到处 INT8 量化模型是 examples/export_int8_model.py；基于校准集生成激活值 scales 是 examples/generate_act_scales.py，用法如下所示:
python examples/generate_act_scales.py \
--model-name <model_name_or_path> \
--output-path <output_act_scales_file_path> \
--num-samples <num_samples> \
--seq-len <sequence_length> \
--dataset-path <path_to_the_calibration_dataset>
2.2 激活值范围统计
激活值范围统计实际是基于校准集去做模型推理，并逐通道统计激活最大值。这里代码实现核心是两个部分，分别是：
- 逐通道计算激活最大值的实现函数
get_act_scales - 为模型的每个 Linear 层添加
stat_input_hook前向钩子。
代码的详细注释如下:
import torch
import torch.nn as nn
from datasets import load_dataset
import functools
from collections import defaultdict
from functools import partial
import numpy as np
from tqdm import tqdm
def get_act_scales(model, tokenizer, dataset_path, num_samples=512, seq_len=512):
"""
逐通道计算模型中每个线性层的激活最大值（绝对值）的尺度，用于后续的量化或归一化处理。
参数:
model (torch.nn.Module): 要分析的PyTorch模型。
tokenizer (PreTrainedTokenizer): 用于将文本转换为模型输入的分词器。
dataset_path (str): 数据集的路径，数据集应为JSON格式。
num_samples (int): 要处理的样本数量，默认512。
seq_len (int): 输入序列的最大长度，默认512。
返回:
act_scales (dict): 包含每个线性层激活最大值的字典，键为层名称，值为对应的最大值张量。
"""
model.eval() # 将模型设置为评估模式，禁用dropout等训练特有的操作
device = next(model.parameters()).device # 获取模型所在的设备（CPU或GPU）
act_scales = {} # 初始化一个字典，用于存储每个层的激活尺度
def stat_tensor(name, tensor):
"""
计算张量的绝对值最大值并更新act_scales字典。
参数:
name (str): 层的名称。
tensor (torch.Tensor): 要统计的张量。
"""
hidden_dim = tensor.shape[-1] # 获取张量的最后一个维度大小（通常是隐藏维度）
tensor = tensor.view(-1, hidden_dim).abs().detach() # 将张量展平并取绝对值
comming_max = torch.max(tensor, dim=0)[0].float().cpu() # 计算每个隐藏维度上的最大值并转移到 CPU
if name in act_scales:
act_scales[name] = torch.max(act_scales[name], comming_max) # 更新最大值
else:
act_scales[name] = comming_max # 初始化最大值
def stat_input_hook(m, x, y, name):
"""
前向钩子函数，用于在每次前向传播时收集输入张量的统计信息。
参数:
m (torch.nn.Module): 当前层的模块。
x (tuple): 输入到当前层的张量。
y (torch.Tensor): 当前层的输出张量。
name (str): 当前层的名称。
"""
if isinstance(x, tuple):
x = x[0] # 如果输入是元组，则取第一个元素
stat_tensor(name, x) # 统计输入张量
hooks = [] # 存储钩子函数，以便后续移除
for name, m in model.named_modules():
if isinstance(m, nn.Linear):
# 对每个线性层注册一个前向钩子，用于统计激活
hooks.append(
m.register_forward_hook(functools.partial(stat_input_hook, name=name))
)
# 加载数据集，假设数据集为JSON格式，包含"text"字段
dataset = load_dataset("json", data_files=dataset_path, split="train")
dataset = dataset.shuffle(seed=42) # 随机打乱数据集
# 遍历指定数量的样本，进行前向传播以收集激活信息
for i in tqdm(range(num_samples), desc="Collecting activation scales"):
input_ids = tokenizer(
dataset[i]["text"], # 获取第i个样本的文本
return_tensors="pt", # 返回PyTorch张量
max_length=seq_len, # 设置最大序列长度
truncation=True # 启用截断
).input_ids.to(device) # 转移到模型所在的设备
model(input_ids) # 前向传播
# 移除所有注册的钩子
for h in hooks:
h.remove()
return act_scales # 返回收集到的激活尺度
有了激活值最大值统计的函数，接下来我们调用这个函数并保存下来即可，使用示例在 generate_act_scales.py，添加中文注释的主要代码如下所示:
@torch.no_grad()
def main():
args = parse_args()
model, tokenizer = build_model_and_tokenizer(args.model_name)
if not os.path.exists(args.dataset_path):
print(f"Cannot find the dataset at {args.dataset_path}")
print("Please download the Pile dataset and put the validation set at the path")
print(
"You can download the validation dataset of the Pile at https://huggingface.co/datasets/mit-han-lab/pile-val-backup/resolve/main/val.jsonl.zst"
)
raise FileNotFoundError
act_scales = get_act_scales(
model, tokenizer, args.dataset_path, args.num_samples, args.seq_len
) # act_scales 是一个字典, key 是层名称
os.makedirs(os.path.dirname(args.output_path), exist_ok=True)
torch.save(act_scales, args.output_path) # 保存统计到的激活值最大值
if __name__ == "__main__":
main()
激活最大值统计字典 act_scales 格式如下所示:
{
"layers.0.self_attn.q_proj": tensor([...]),
"layers.0.self_attn.k_proj": tensor([...]),
# ... 其他层
}
2.3 离群值平滑
计算平滑因子 $s$（代码中也命名为 scales）计算公式为 $s_j = \frac{\max(\vert \mathbf{X}_j\vert)^{\alpha}}{\max(\vert \mathbf{W}_j\vert )^{1 - \alpha}}$，上一个模块已经逐通道统计了激活最大值 scales，再逐通道计算下权重矩阵的最大值，结合 $s_j$ 公式就可以得到平滑因子 $s$ 了，代码如下所示:
# 为了更方便理解，我做了一些简化
# 如果 fcs 是线性层列表，则取整体的最大值，用来计算平滑因子 scales。
weight_scales = torch.cat([fc.weight.abs().max(dim=0, keepdim=True)[0] for fc in fcs], dim=0)
weight_scales = weight_scales.max(dim=0)[0].clamp(min=1e-5)
scales = (act_scales.pow(alpha) / weight_scales.pow(1 - alpha) # 平滑因子 s
有了平滑因子，就可以实现离群值平滑了，其本质上是通过将激活难度转移至权重来实现的，公式表现为 $diag(s) * W$。同时为了，同时考虑到输入 $X$ 通常由前面的线性操作（如线性层、层归一化等）产生，我们可以轻松地将平滑因子离线地融合到前一层的参数中 $diag(s)\ast W_{Pre}$，不会因额外的缩放操作而导致增加内核调用开销。离群值平滑的核心代码如下所示:
# 将平滑因子离线地融合到前一层的参数中
ln.weight.div_(scales)
ln.bias.div_(scales)
# 将当前层的激活值量化难度转移至权重
for fc in fcs:
fc.weight.mul_(scales.view(1, -1))
上述分析和代码描述其实更多的是体现 smooth 平滑算法如何实现的，但是在具体应用上其实有很多细节问题需要我们搞懂，比如我们知道对于自回归 llm，我们量化的主要是 self-attention 和 和 mlp 模块中的线性层，但是这里有一些细节需要注意：
attention和mlp的里面线性层是否都需要平滑，看代码发现 attention 的 output 和 mlp 的 down 线性层权重没有做更新；（推测是一个模块的最前面的线性层才需要做权重更新？）attention的 q_linear、k_linear、v_linear 是共用一个激活 scales，即 attention 的输入 scales[“*.attention.q_proj”]，这个应该很明显，因为这这三个线性层的输入就是同一个。mlp的 3 个线性层的 up_linear、gatp_linear、down_linear 是共用一个激活 scales 吗，即 mlp 的输入 scales[“*.mlp.gate_proj”]，这个也很明显，up_linear 和 gatp_linear 的输入也是一样的。- 输入是同一个的线性层可以共享量化因子 $s$。
针对平滑 llama 模型的 smooth 代码如下所示:
# 代码做了一些简化，保留核心
@torch.no_grad()
def smooth_ln_fcs_llama_like(ln, fcs, act_scales, alpha=0.5):
"""
针对LLaMA-like模型的层归一化和平滑全连接层的函数。
参数:
ln (LlamaRMSNorm, MistralRMSNorm, MixtralRMSNorm): 要平滑的层归一化层，适用于LLaMA-like模型。
fcs (nn.Linear 或 list of nn.Linear): 要平滑的一个或多个全连接层。
act_scales (torch.Tensor): 激活的尺度信息，与层归一化的权重数量相同。
alpha (float): 平滑因子，用于控制激活尺度和权重尺度的平衡，默认0.5。
返回:
None: 该函数直接修改传入的层归一化和全连接层的权重。
"""
# 确保fcs是一个列表
if not isinstance(fcs, list):
fcs = [fcs]
# 确保ln是LlamaRMSNorm, MistralRMSNorm或MixtralRMSNorm的实例
assert isinstance(ln, (LlamaRMSNorm, MistralRMSNorm, MixtralRMSNorm)), \
"ln必须是LlamaRMSNorm, MistralRMSNorm或MixtralRMSNorm的实例"
# 检查每个全连接层是否为nn.Linear，并且ln的权重数量与fc的输入特征数及act_scales数量一致
for fc in fcs:
assert isinstance(fc, nn.Linear), "fcs必须是nn.Linear的实例"
assert ln.weight.numel() == fc.in_features == act_scales.numel(), \
"ln的权重数量、fc的输入特征数和act_scales的数量必须相同"
# 获取设备和数据类型，以便将act_scales转换到相同的设备和类型
device, dtype = fcs[0].weight.device, fcs[0].weight.dtype
act_scales = act_scales.to(device=device, dtype=dtype)
# 计算每个全连接层权重的最大绝对值，按隐藏维度汇总
weight_scales = torch.cat(
[fc.weight.abs().max(dim=0, keepdim=True)[0] for fc in fcs], dim=0
)
# 选择每个隐藏维度上的最大权重尺度，并确保其最小值为1e-5以避免除零错误
weight_scales = weight_scales.max(dim=0)[0].clamp(min=1e-5)
# 计算平滑尺度，结合激活尺度和权重尺度
scales = (
(act_scales.pow(alpha) / weight_scales.pow(1 - alpha))
.clamp(min=1e-5) # 确保尺度的最小值为1e-5
.to(device)
.to(dtype)
)
# 调整层归一化的权重
ln.weight.div_(scales)
# 调整全连接层的权重
for fc in fcs:
fc.weight.mul_(scales.view(1, -1))
@torch.no_grad()
def smooth_lm(model, scales, alpha=0.5):
"""
遍历模型中的所有解码器层，应用平滑层归一化和全连接层的操作。
参数:
model (torch.nn.Module): 要平滑的模型。
scales (dict): 包含各层激活尺度的字典，键为层名称，值为对应的激活尺度张量。
alpha (float): 平滑因子，用于控制激活尺度和权重尺度的平衡，默认0.5。
返回:
None: 该函数直接修改模型中的层归一化和全连接层的权重。
"""
# 遍历模型中的所有模块
for name, module in model.named_modules():
# 针对LlamaDecoderLayer和MistralDecoderLayer类型的模块
if isinstance(module, (LlamaDecoderLayer, MistralDecoderLayer)):
# 获取自注意力层的层归一化层
attn_ln = module.input_layernorm
# 获取自注意力层的Q, K, V全连接层
qkv = [
module.self_attn.q_proj,
module.self_attn.k_proj,
module.self_attn.v_proj,
]
# 获取对应的激活尺度
qkv_input_scales = scales[name + ".self_attn.q_proj"]
# 应用针对LLaMA-like模型的平滑函数
smooth_ln_fcs_llama_like(attn_ln, qkv, qkv_input_scales, alpha)
# 获取前馈网络的层归一化层和全连接层
ffn_ln = module.post_attention_layernorm
fcs = [module.mlp.gate_proj, module.mlp.up_proj]
# 获取对应的激活尺度
fcs_input_scales = scales[name + ".mlp.gate_proj"]
# 应用针对LLaMA-like模型的平滑函数
smooth_ln_fcs_llama_like(ffn_ln, fcs, fcs_input_scales, alpha)
2.4 伪量化推理
对应代码在 fake_quant.py 中，主要包括两个过程，对应代码在 fake_quant.py：
- FP32 模型转换为 INT8 模型，对应权重量化函数
from_float， 并构建W8A8Linear类； - 伪量化推理，因为是伪量化推理，所以这里没有量化层替换 FP32 层的操作，模型结构和以前一模一样，推理函数 forward 也比较简单，只是加了
quant操作用于验证激活量化函数的正确性。
前面我们计算激活最大值和平滑因子 $s$ 都是逐通道计算的，因为这是确保量化精度的必要条件，但是权重和激活量化的模式我们是可以调整的，以动态调整性能和量化推理精度，具体实现和区别在第一章已经详细描述了，这里不再描述。这部分功能的核心就是在于实现 W8A8Linear 类，其中 from_float 实现对权重的量化函数，forward 函数对激活量化为了评估量化正确性。
为了方便理解代码，我只保留了针对 llama 模型权重量化转换和量化推理的部分，添加中文详细注释后的代码如下所示：
import torch
from torch import nn
from functools import partial
@torch.no_grad()
def quantize_weight_per_channel_absmax(w, n_bits=8):
"""
按通道使用绝对最大值进行权重量化。
参数:
w (torch.Tensor): 权重张量，形状为 (out_features, in_features)。
n_bits (int): 量化位数，默认为8。
返回:
torch.Tensor: 量化后的权重张量。
"""
scales = w.abs().max(dim=-1, keepdim=True)[0] # 计算每个输出通道的绝对最大值
q_max = 2 ** (n_bits - 1) - 1 # 计算量化的最大值，例如8位量化的最大值为 127
scales.clamp_(min=1e-5).div_(q_max) # 防止除以零，将最小尺度限制为1e-5，并计算缩放因子
w.div_(scales).round_().mul_(scales) # 对权重进行缩放、四舍五入，并通过 .mul_(scales) 操作重新缩放回原始尺度
return w
@torch.no_grad()
def quantize_activation_per_token_absmax(t, n_bits=8):
"""
按每个token的绝对最大值进行激活量化。
参数:
t (torch.Tensor): 激活张量，形状通常为 (batch_size, seq_len, hidden_size)。
n_bits (int): 量化位数，默认为8。
返回:
torch.Tensor: 量化后的激活张量。
"""
t_shape = t.shape
t = t.view(-1, t_shape[-1]) # 将张量重塑为 (batch_size * seq_len, hidden_size) 以便逐token量化
scales = t.abs().max(dim=-1, keepdim=True)[0] # 计算每个token的绝对最大值
q_max = 2 ** (n_bits - 1) - 1 # 计算量化的最大值，例如8位量化的最大值为127
scales.clamp_(min=1e-5).div_(q_max) # 防止除以零，将最小尺度限制为1e-5，并计算缩放因子
t.div_(scales).round_().mul_(scales) # 对激活进行缩放、四舍五入并重新缩放回原始尺度
t = t.view(t_shape) # 恢复原始形状
return t
class W8A8Linear(nn.Module):
"""
一个自定义的8位权重量化和8位激活量化的线性层。
参数:
in_features (int): 输入特征数。
out_features (int): 输出特征数。
bias (bool): 是否使用偏置，默认为True。
act_quant (str): 激活量化方式，可选 "per_token" 或 "per_tensor"，默认为 "per_token"。
quantize_output (bool): 是否量化输出，默认为False。
"""
def __init__(
self,
in_features,
out_features,
bias=True,
act_quant="per_token",
quantize_output=False,
):
super().__init__()
self.in_features = in_features
self.out_features = out_features
# 初始化权重为随机数，使用半精度浮点数，并不需要梯度
self.register_buffer(
"weight",
torch.randn(
self.out_features,
self.in_features,
dtype=torch.float16,
requires_grad=False,
),
)
# 初始化偏置为零，如果需要偏置
if bias:
self.register_buffer(
"bias",
torch.zeros(
(1, self.out_features), dtype=torch.float16, requires_grad=False
),
)
else:
self.register_buffer("bias", None)
# 根据act_quant参数选择激活量化函数
if act_quant == "per_token":
self.act_quant_name = "per_token"
self.act_quant = partial(quantize_activation_per_token_absmax, n_bits=8)
elif act_quant == "per_tensor":
self.act_quant_name = "per_tensor"
self.act_quant = partial(quantize_activation_per_tensor_absmax, n_bits=8)
else:
raise ValueError(f"Invalid act_quant: {act_quant}")
# 根据quantize_output参数决定是否量化输出
if quantize_output:
self.output_quant_name = self.act_quant_name
self.output_quant = self.act_quant
else:
self.output_quant_name = "None"
self.output_quant = lambda x: x # 如果不量化输出，保持不变
def to(self, *args, **kwargs):
"""
重载to方法，以确保权重和偏置也随模块一起移动到指定设备和类型。
"""
super(W8A8Linear, self).to(*args, **kwargs)
self.weight = self.weight.to(*args, **kwargs)
if self.bias is not None:
self.bias = self.bias.to(*args, **kwargs)
return self
@torch.no_grad()
def forward(self, x):
"""
前向传播，先量化激活，然后执行线性变换，最后量化输出（如果需要）。
参数:
x (torch.Tensor): 输入张量，形状通常为 (batch_size, seq_len, in_features)。
返回:
torch.Tensor: 输出张量，形状为 (batch_size, seq_len, out_features)。
"""
# 量化输入激活
q_x = self.act_quant(x)
# 执行线性变换
y = torch.functional.F.linear(q_x, self.weight, self.bias)
# 量化输出激活（如果需要）
q_y = self.output_quant(y)
return q_y
@staticmethod
@torch.no_grad()
def from_float(
module, weight_quant="per_channel", act_quant="per_token", quantize_output=False
):
"""
从浮点型线性层创建一个量化后的 W8A8 Linear层。
参数:
module (nn.Linear): 要量化的浮点型线性层。
weight_quant (str): 权重量化方式，可选 "per_channel" 或 "per_tensor"，默认为 "per_channel"。
act_quant (str): 激活量化方式，可选 "per_token" 或 "per_tensor"，默认为 "per_token"。
quantize_output (bool): 是否量化输出，默认为False。
返回:
W8A8Linear: 量化后的线性层。
"""
assert isinstance(module, torch.nn.Linear), "module必须是torch.nn.Linear的实例"
# 创建一个新的W8A8Linear实例
new_module = W8A8Linear(
module.in_features,
module.out_features,
bias=module.bias is not None,
act_quant=act_quant,
quantize_output=quantize_output,
)
# 量化权重
if weight_quant == "per_channel":
new_module.weight = quantize_weight_per_channel_absmax(
module.weight.clone(), n_bits=8
) # 使用8位按通道量化
elif weight_quant == "per_tensor":
new_module.weight = quantize_weight_per_tensor_absmax(
module.weight.clone(), n_bits=8
) # 使用8位按张量量化
else:
raise ValueError(f"Invalid weight_quant: {weight_quant}")
new_module.weight_quant_name = weight_quant
# 如果有偏置，直接复制
if module.bias is not None:
new_module.bias = module.bias.clone()
return new_module
def __repr__(self):
"""
自定义模块的字符串表示，显示量化参数。
"""
return f"W8A8Linear({self.in_features}, {self.out_features}, bias={self.bias is not None}, weight_quant={self.weight_quant_name}, act_quant={self.act_quant_name}, output_quant={self.output_quant_name})"
@torch.no_grad()
def quantize_llama_like(
model, weight_quant="per_channel", act_quant="per_token", quantize_bmm_input=False
):
"""
对LLaMA-like模型进行量化。
参数:
model (nn.Module): 要量化的LLaMA-like模型。
weight_quant (str): 权重量化方式，可选 "per_channel" 或 "per_tensor"，默认为 "per_channel"。
act_quant (str): 激活量化方式，可选 "per_token" 或 "per_tensor"，默认为 "per_token"。
quantize_bmm_input (bool): 是否量化批量矩阵乘法的输入，默认为False。
返回:
nn.Module: 量化后的LLaMA-like模型。
"""
from transformers.models.llama.modeling_llama import (
LlamaAttention,
LlamaMLP,
)
from transformers.models.mistral.modeling_mistral import (
MistralAttention,
MistralMLP,
)
# 遍历模型中的所有模块
for name, m in model.model.named_modules():
if isinstance(m, (LlamaMLP, MistralMLP)):
# 量化MLP层中的gate_proj, up_proj和down_proj
m.gate_proj = W8A8Linear.from_float(
m.gate_proj, weight_quant=weight_quant, act_quant=act_quant
)
m.up_proj = W8A8Linear.from_float(
m.up_proj, weight_quant=weight_quant, act_quant=act_quant
)
m.down_proj = W8A8Linear.from_float(
m.down_proj, weight_quant=weight_quant, act_quant=act_quant
)
elif isinstance(m, (LlamaAttention, MistralAttention)):
# 量化注意力层中的q_proj, k_proj, v_proj以及o_proj
m.q_proj = W8A8Linear.from_float(
m.q_proj,
weight_quant=weight_quant,
act_quant=act_quant,
quantize_output=quantize_bmm_input,
)
m.k_proj = W8A8Linear.from_float(
m.k_proj,
weight_quant=weight_quant,
act_quant=act_quant,
quantize_output=quantize_bmm_input,
)
m.v_proj = W8A8Linear.from_float(
m.v_proj,
weight_quant=weight_quant,
act_quant=act_quant,
quantize_output=quantize_bmm_input,
)
m.o_proj = W8A8Linear.from_float(
m.o_proj, weight_quant=weight_quant, act_quant=act_quant
)
return model
2.5 INT8 量化推理
对应代码在 opt.py，代码实现其实主要包括两个过程：
- FP32 模型转换为 INT8 模型，核心是实现权重的量化函数；
- INT8 量化 kernel 替换原来的 FP32 kernel，再执行原来一样的模型推理过程。
第一步在代码实现上跟伪量化基本一样，都是实现权重量化函数 from_float，区别只在于不再将输入缩放回原始尺度，代码如下所示:
@torch.no_grad()
def quantize_weight_per_channel_absmax(w):
# w: [out_channel, in_channel]
scales = w.abs().max(dim=1)[0] / 127
scales = scales.view(-1, 1)
if not w.is_cuda:
# half rounding is not supported on CPU
w = w.float()
# use inplace operation to save memory
w.div_(scales).round_().clamp_(-128, 127)
w_q = w.to(torch.int8)
return w_q, scales
然后就是来创建自定义的 INT8 量化线性层，并用量化层替换模型中原来的浮点层，这里的难点在于要学会用 cuda/triton 编写 INT8 量化 kernel，作者基于 cutlass 库实现了多种量化线性层 kernel。python 版的量化 W8A8B8O8Linear 类实现如下所示:
class W8A8B8O8Linear(nn.Module):
"""
一个自定义的8位权重量化、8位激活量化、8位偏置量化和8位输出量化的线性层。
参数:
in_features (int): 输入特征数。
out_features (int): 输出特征数。
alpha (float): 输入缩放因子，默认为1.0。
beta (float): 偏置缩放因子，默认为1.0。
"""
def __init__(self, in_features, out_features, alpha=1.0, beta=1.0):
super().__init__()
self.in_features = in_features
self.out_features = out_features
# 注册量化后的权重为 int8 类型的缓冲区，不参与梯度计算
self.register_buffer('weight', torch.randint(-127, 127, (self.out_features,
self.in_features), dtype=torch.int8, requires_grad=False))
# 注册量化后的偏置为 int8 类型的缓冲区，不参与梯度计算
self.register_buffer('bias', torch.zeros(
(1, self.out_features), dtype=torch.int8, requires_grad=False))
# 注册输入缩放因子和偏置缩放因子
self.register_buffer('a', torch.tensor(alpha))
self.register_buffer('b', torch.tensor(beta))
def to(self, *args, **kwargs):
"""
重载to方法，以确保权重和偏置也随模块一起移动到指定设备和类型。
"""
super().to(*args, **kwargs)
self.weight = self.weight.to(*args, **kwargs)
self.bias = self.bias.to(*args, **kwargs)
self.a = self.a.to(*args, **kwargs)
self.b = self.b.to(*args, **kwargs)
return self
@torch.no_grad()
def forward(self, x):
"""
前向传播，执行量化后的线性变换。
参数:
x (torch.Tensor): 输入张量，形状通常为 (batch_size, seq_len, in_features)。
返回:
torch.Tensor: 输出张量，形状为 (batch_size, seq_len, out_features)。
"""
x_shape = x.shape
# 将输入重塑为 (batch_size * seq_len, in_features) 以便进行批量矩阵乘法
x = x.view(-1, x_shape[-1])
# 调用自定义的量化线性变换函数
y = linear_a8_w8_b8_o8(x, self.weight, self.bias,
self.a.item(), self.b.item())
# 恢复原始的输入形状
y = y.view(*x_shape[:-1], -1)
return y
@staticmethod
@torch.no_grad()
def from_float(module: nn.Linear, input_scale, output_scale):
"""
从浮点型线性层创建一个量化后的W8A8B8O8Linear层。
参数:
module (nn.Linear): 要量化的浮点型线性层。
input_scale (float): 输入缩放因子。
output_scale (float): 输出缩放因子。
返回:
W8A8B8O8Linear: 量化后的线性层。
"""
# 创建一个新的量化线性层实例
int8_module = W8A8B8O8Linear(
module.in_features, module.out_features)
# 量化权重，并获取缩放因子
int8_weight, weight_scale = quantize_per_tensor_absmax(module.weight)
# 量化偏置，并获取缩放因子
int8_bias, bias_scale = quantize_per_tensor_absmax(module.bias)
# 计算输入缩放因子 alpha 和偏置缩放因子 beta
alpha = input_scale * weight_scale / output_scale
beta = bias_scale / output_scale
# 设置量化后的权重和偏置
int8_module.weight = int8_weight
int8_module.bias = int8_bias
# 设置缩放因子
int8_module.a = alpha
int8_module.b = beta
return int8_module
def __repr__(self):
"""
自定义模块的字符串表示，显示量化参数。
"""
return f"W8A8B8O8Linear({self.in_features}, {self.out_features}, alpha={self.a.item()}, beta={self.b.item()})"
看出区别没，和前面不同，真正的线性量化 kernel 的 forward 是没有使用 pytorch 的 torch.functional.F.linear 函数的，而是使用自行变形的 INT8 kernel 函数 linear_a8_w8_b8_o8。值的注意的是线性层的量化 kernel 有多重形式，作者提供了如下形式:
linear_a8_w8_b8_o8：激活、权重、bias 和输出都是 INT8，属于完全的量化 kernel。W8A8B8O8LinearReLU: 激活、权重、bias 和输出都是 INT8，且和 relue 算子做了融合！W8A8BFP32OFP32Linear和linear_a8_w8_b32_o32_with_scaling：激活、权重是 INT8，bias 是 FP32，输出是 FP32，前者对权重做平滑后者没有。W8A8BFP32OFP32Linear。W8A16Linear：权重 INT8，激活是FP16，forward 使用的是torch.functional.F.linear，运算依然是浮点操作。
之所以提供这么多中选择，我推测是因为 llm 种类繁多，可能存在特定 int8 线性层导致模型精度降低的可能情况，找到了在那个层，用 W8A16Linear 或者 FP32 层替换，从而可解决量化导致掉点的问题。
再让我们快速看下 linear_a8_w8_b8_o8 量化 kernel 的 cuda 实现代码。
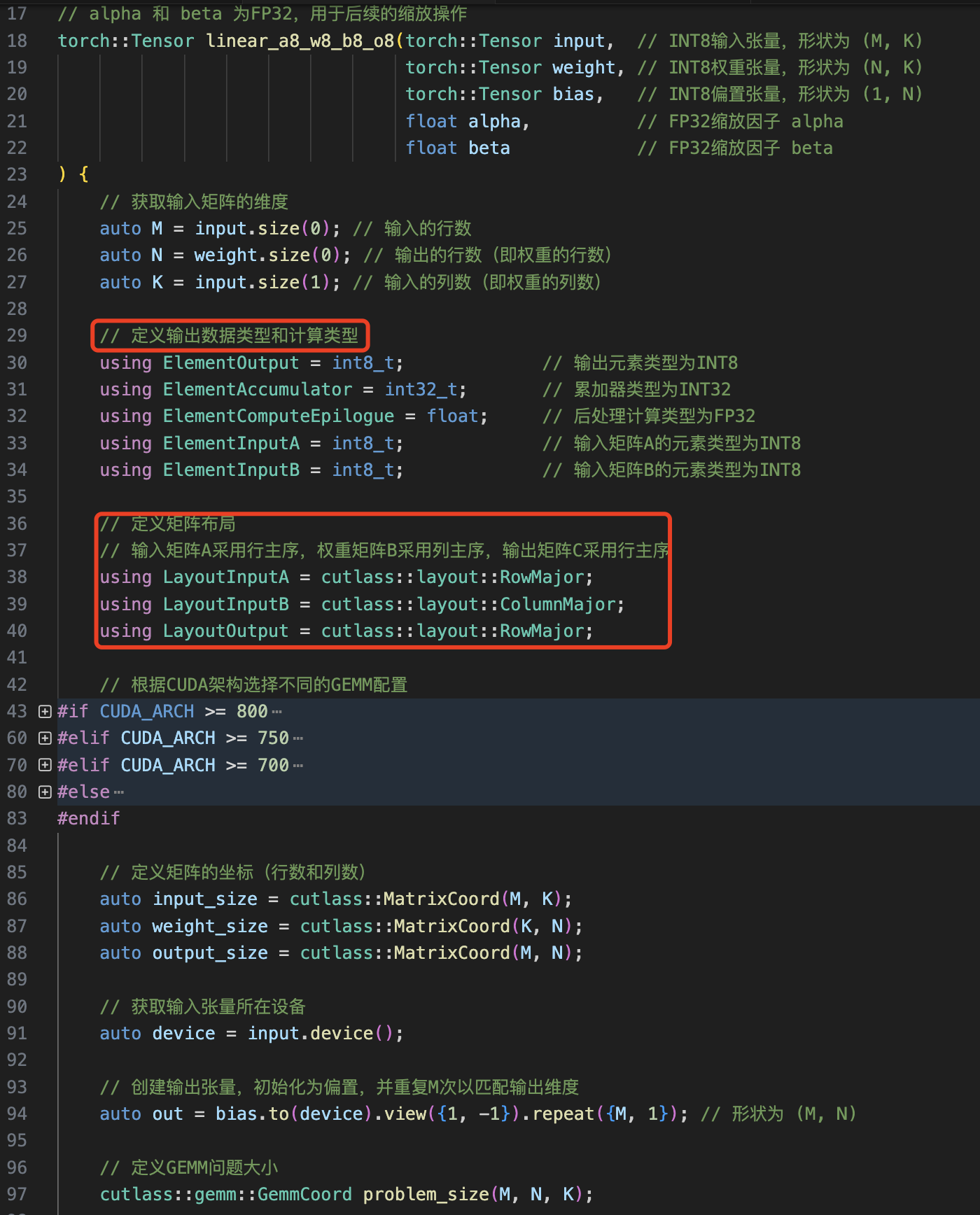
了解了量化 kernel 种类和定义，我们再回过头来量化模型是如何实现的，通过阅读代码会发现量化模型是一个全新的模型，除了模型结构和原来浮点模型一样，但是在实现上已经是全新了，省略版代码如下所示：
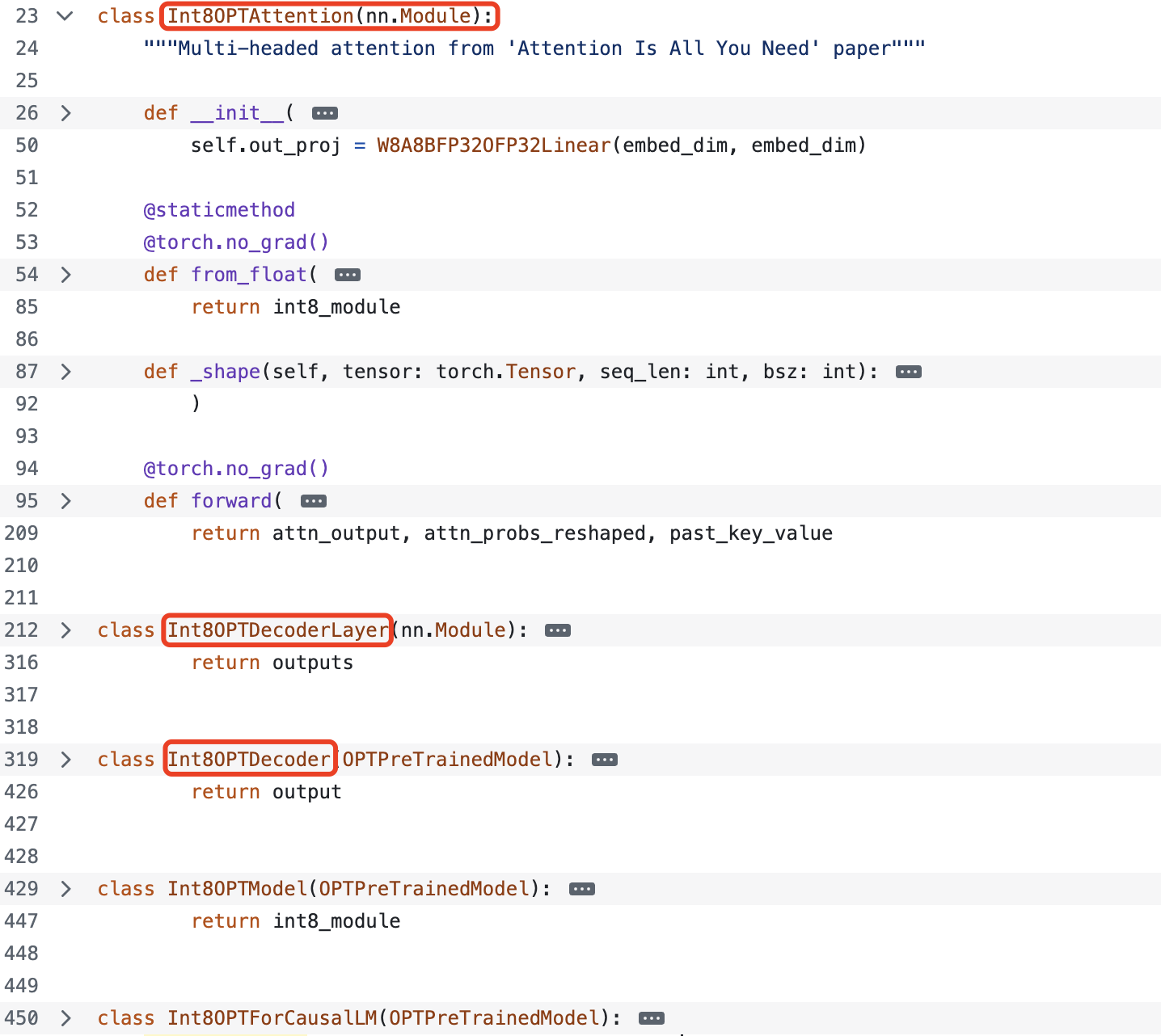
将 Attention 和 MLP（decoder）中相关 FP32 kernel 替换为量化 kernel，即重新定义了模型结构，哪些层需要量化和论文图 6 以及第一节提到的量化范围一样，代码如下所示:
# 下述代码做了省略
class Int8OPTAttention(nn.Module):
"""Multi-headed attention from 'Attention Is All You Need' paper"""
def __init__(
self,
embed_dim: int,
num_heads: int,
):
super().__init__()
self.qk_bmm = BMM_S8T_S8N_F32T(1.0)
self.pv_bmm = BMM_S8T_S8N_S8T(1.0)
self.k_proj = W8A8B8O8Linear(embed_dim, embed_dim)
self.v_proj = W8A8B8O8Linear(embed_dim, embed_dim)
self.q_proj = W8A8B8O8Linear(embed_dim, embed_dim)
self.out_proj = W8A8BFP32OFP32Linear(embed_dim, embed_dim) # 最后一个线性层的输出是 fp32，以适应后面的 ln 层的计算
class Int8OPTDecoderLayer(nn.Module):
def __init__(self, embed_dim, num_attention_heads, ffn_dim):
super().__init__()
self.embed_dim = embed_dim
self.self_attn = Int8OPTAttention(
embed_dim=self.embed_dim, num_heads=num_attention_heads
)
self.self_attn_layer_norm = LayerNormQ(self.embed_dim)
self.fc1 = W8A8B8O8LinearReLU(self.embed_dim, ffn_dim) # 和 relue 做了融合的量化层，权重、激活（输入）、输出都是 INT8
self.fc2 = W8A8BFP32OFP32Linear(ffn_dim, self.embed_dim) # 最后一个线性层的输出是 fp32
self.final_layer_norm = LayerNormQ(self.embed_dim) # 加了 quantize 操场的 LN
值的注意的是，这里的 self_attn_layer_norm 实际是融合了量化操作的，所以这是名字后面加了 Q 的原因，其实现代码如下所示:
class LayerNormQ(torch.nn.Module):
def __init__(self, dim, eps=1e-5):
super().__init__()
self.input_scale = 1.0
self.eps = eps
self.register_buffer('weight', torch.ones(dim, dtype=torch.float32))
self.register_buffer('bias', torch.zeros(dim, dtype=torch.float32))
def forward(self, x):
# 将 输入转换为和权重一样的数据类型，但其实在论文图 6 可以看出 mlp 的最后一个线性层输出已经是 fp32 类型
x = x.to(self.weight.dtype)
ln_output_fp = torch.nn.functional.layer_norm(
x, x.shape[-1:], self.weight, self.bias, self.eps)
# 将 layer_norm 的 fp32 输出结果量化为 INT8，也就是对应 quantize 层，只是这里融合进了 layer_norm 里面
ln_output_int8 = ln_output_fp.round().clamp(-128, 127).to(torch.int8)
return ln_output_int8
三 总结
致此，smoothquant 仓库的源码解析已经全部完成，个人经验是读论文更多的是了解算法原理和公式推导，但是真的应用和细节还是得看源码。最后我们再总结下 smoothquant 仓库，其主要分三个部分：
- 基于校准集统计激活最大值
calibration.py； - 激活难度迁移至权重的平滑模块
smooth.py; - 包含模型权重转换的伪量化推理
fake_quant.py和真正量化推理opt.py。
参考资料
- [源码] [万字] SmoothQuant量化深入探究
- https://github.com/mit-han-lab/smoothquant/
- https://github.com/Guangxuan-Xiao/torch-int/