AWQ 量化详解

Categories: LLM_Compression 2024-11-01

• 1. 摘要
• 2. AWQ: 激活感知的权重量化
  • 2.1 观点 1-权重并非同等重要，需要基于激活分布来挑选权重的显著通道
  • 2.2 观点 2-对显著权重进行放大可以降低量化误差
  • 2.3 算法-计算缩放因子 s
• 3. 实验
• 4. 结论
• 参考资料

先回顾下 SmoothQuant 论文提到的几个关键总结：

1. 激活比权重更难量化。
2. 激活值中的离群值是导致大模型难以量化的重要因素。
3. 激活离群值通常出现于特定通道。

可以发现 SmoothQuant 核心是解决了 LLM 激活难以量化的问题。而 AWQ 论文是 SmoothQuant 的进一步发展，核心作者都是同一批人，那么 AWQ 论文的核心是什么呢？不会是优化权重量化吧。

1. 摘要

本文提出了激活感知权重量化 (AWQ)，这是一种适合硬件的 LLM 低位权重（比如 w4）量化方法。AWQ 发现，并非所有 LLM 权重都同等重要，仅保护 1% 的显著权重便能大幅减少量化误差。而要识别显著权重通道，需要参考的是激活分布而非权重本身分布。为了避免硬件效率低下的混合精度量化，我们通过数学推导得出，放大显著通道可以减少量化误差。AWQ 采用等效变换来放大显著权重通道，用于保留权重显著通道值，保留的比例通过离线收集激活统计数据确定。

AWQ 不依赖反向传播或重构，因此可以泛化到不同领域和模态而不会对校准集过拟合。AWQ 在各种语言建模和领域特定的基准测试（编码和数学）中优于现有方法。凭借更好的泛化性，它在指令微调语言模型以及多模态语言模型上首次实现了卓越的量化性能，多模态模型量化是前作 SmoothQuant 没有测试的领域。

此外，作者还开发了 TinyChat，一个高效灵活的 4 位设备端 LLM/VLM 推理框架。通过内核融合和平台适应的权重打包，TinyChat 在桌面和移动 GPU 上相比 Huggingface FP16 实现了超过 3 倍的加速，并使 70B 参数的 Llama-2 模型在移动 GPU 上的部署成为可能。

值得注意的是，虽然作者开发的 TinyChat 使用的是 w4 量化，但理论上不考虑精度的前提下，量化位数可以是 3、2、1 任意低比特位数。

2. AWQ: 激活感知的权重量化

AWQ: ACTIVATION-AWARE WEIGHT QUANTIZATION

在本节中，作者首先提出了一种仅针对权重的量化方法，通过保护更多“重要”权重，在无需训练或回归的情况下提升模型准确性。并开发了一种数据驱动的方法，来搜索能够减少量化误差的最佳缩放比例（见图 2）。

图 2b 展示了可以基于激活分布找到 LLM 中 1% 的关键权重，将这些关键权重保留为 FP16 可以显著提升量化后的性能（困惑度从 43.2（左图）降至 13.0（中图））。但这种混合精度格式在硬件上效率较低，基于激活感知原则，作者提出了 AWQ（右图）。AWQ 采用逐通道缩放方式，保护关键权重并减少量化误差。作者测试了 OPT-6.7B 模型上使用 INT3-g128 量化下的困惑度 PPL(越小越好)表现为 13.0，和前面的混合精度量化一样，说明 AWQ 量化算法有效。

2.1 观点 1-权重并非同等重要，需要基于激活分布来挑选权重的显著通道

作者观察到，LLM 中的权重并非同等重要：仅有 0.1%~1% 的小部分显著权重对模型输出精度影响较大。如果能保留这部分关键权重，其他权重使用低比特量化推理，那么就能在保持模型精度的前提下，大幅降低模型内存占用和提高推理速度。

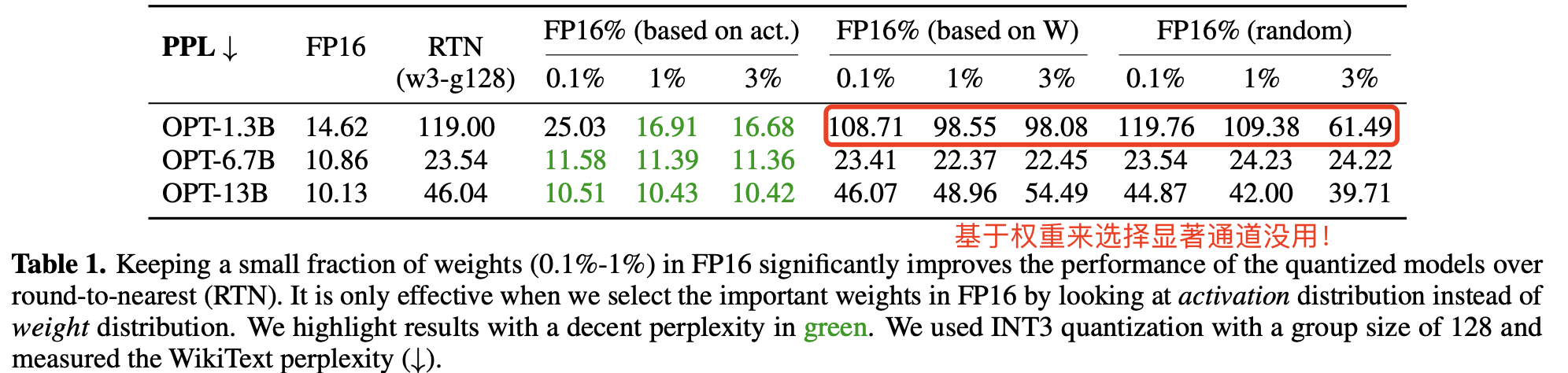
这里有个问题是，哪部分权重通道更重要呢？通常评估权重重要性的方法是查看其大小或 L2-范数 (Han 等，2015；Frankle 和 Carbin，2018)，但在量化推理中也是这样吗？为此，作者做了三个对比实验来判断挑选显著权重方法的有效性，结果发现保留大范数的权重通道（即基于 W 的 FP16%）对量化性能的提升有限，跟随机选择通道带来的提升类似。详细对比结果见表 1 所示：

但有趣的是，基于激活幅度来选择权重可以显著提升性能！即使只保留 0.1%-1% 的通道为 FP16。作者推测是，幅度较大的输入特征通常更重要，保留相应的权重为 FP16 可以更好地保护这些特征，从而提升模型性能。

具体实现上，作者是对激活值的每一列求绝对值的平均值，然后把平均值较大的一列对应的通道视作显著通道，保留 FP16 精度。

到这里可以总结出一个重要结论：LLM 权重并非同等重要，只有 0.1%~1% 的小部分显著权重对模型输出精度影响较大，又因为幅度较大的输入特征通常更重要，因此需要基于激活分布来挑选权重的显著通道。

局限性：尽管保留 0.1% 的权重为 FP16 可以提升量化性能，且不会显著增加模型的总位数，但混合精度的数据类型会推理系统实现复杂化。因此还需要找到一种方法，可以保护这些关键权重同时又不用实际保留它们为 FP16。

2.2 观点 2-对显著权重进行放大可以降低量化误差

论文描述是基于激活感知缩放保护关键权重 Protecting Salient Weights by Activation-aware Scaling，不是很清楚，这里我换了一种表达。

作者提出一种替代方案，通过逐通道缩放减少关键权重的量化误差，避免硬件效率问题。

量化误差分析

从权重量化带来的误差分析入手。假设一个权重组或块 $\mathbf{w}$，其线性操作可写为 $y = \mathbf{wx}$，而量化后的对应形式为 $y = Q(\mathbf{w})\mathbf{x}$，由此可定义量化函数为：

其中，$N$ 是量化位数，$\Delta$ 是由绝对值的最大值决定的量化缩放系数。

现在考虑对于一个权重元素 $w \in \mathbf{w}$，如果我们引入缩放因子 $s$，并在量化过程中将权重 $w$ 与 $s$ 相乘，同时将激活 $x$ 以同样的缩放因子 $s$ 逆向缩放！即 $Q(w \cdot s)(x / s)$，函数形式为：

虽然公式 1 和公式 2 在数学上是“等效”的，但是带来的精度损失是不一样的。

$\Delta’$ 是在应用 $s$ 之后的新量化缩放系数。作者通过实验发现：

1. 来自 $\text{Round}(\cdot)$ 的期望误差（记为 $\text{RoundErr}(\cdot)$）不变：由于舍入函数将浮点数映射到整数，误差大致在 $[0, 0.5]$ 范围内均匀分布，导致平均误差约为 0.25，即 $\text{RoundErr}(\cdot) \sim 0.25$。
2. 对单个元素 $w$ 进行缩放通常不会改变 $\mathbf{w}$ 组的最大值。因此可以得出 $\Delta’ \approx \Delta$ 的结论；
3. 由于 $\Delta$ 和 $x$ 以 FP16 表示，因此它们没有量化误差。

因此，方程 (1) 和 (2) 中的量化误差可以表示为公式（3）：

两个误差相除，可得新误差与原始误差的比率为 $\frac{\Delta{\prime}}{\Delta} \cdot \frac{1}{s}$。因为 $\Delta{\prime} \approx \Delta$ 且 $s > 1$，则可推公式（2）的误差小于公式（1），由此，作者认为量化时对显著权重进行放大，可以降低量化误差。

到这里，论文是通过公式推导证明了观点 2 的由来，下面才是实验证明。

但是前面的设想和公式推导还只是理论层面，因此为了验证该想法，作者在 OPT-6.7B 模型的 1% 显著通道上乘以 $s > 1$，并做了相关对比实验，实验结果在表 2 中。

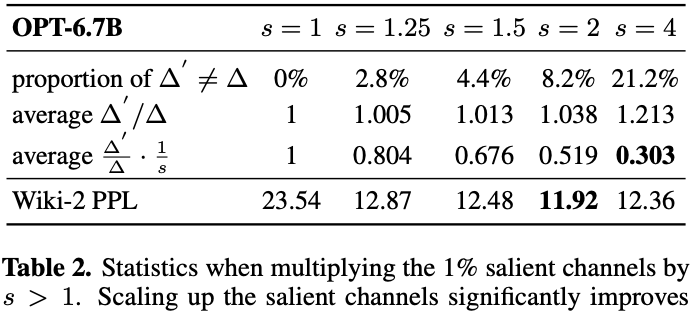
先看直接结果（模型精度变化），结果显示，放大显著通道非常有效：模型困惑度 PPL 从 $s = 1$ 时的 23.54（仅为 RTN）降低到 $s = 2$ 时的 11.92。

再看间接结果：

• 随着 $s$ 增加，$\Delta \ne \Delta’$ 的比例逐渐增大，但在 $s < 2$ 时比例还是很低的(<5%)；
• 误差比值 $\frac{\Delta{\prime}}{\Delta} \cdot \frac{1}{s}$ 随 $s$ 增加持续减小，符合前面的推导。

有点意外的是，最佳困惑度在 $s = 2$ 时出现而不是 $4$（s = 4 时误差比值最小）。作者因为如果 $s$ 过大，$\Delta$ 增加会放大非显著通道的相对误差（非显著通道的误差会被 $\frac{\Delta{\prime}}{\Delta}$ 放大，在 $s = 4$ 时 21.2% 的通道比率大于 1），从而可能影响模型整体精度。因此，在保护显著通道时，我们还需考虑非显著通道的误差。

到此，表 2 的实验结果证明了量化时对显著权重进行放大，是可以降低量化误差的，同时，在保护显著通道时，我们还需考虑非显著通道的误差。

如何选取 $s$ 来平衡显著通道和非显著通道的误差，就是下一节内容了，也是这篇论文相对前作的核心贡献，毕竟权重乘以缩放因子的方法 smoothquant 论文已经提出了，这节更多的是通过公式推导和实验证明了权重乘以 $> 1$ 的缩放因子可以降低（权重）量化误差！而前作 smoothquant 针对权重乘以缩放因子 $s$ 就可以将激活量化难度转移至权重（实际就是降低量化误差）并没有给出一个很详细的理论说明和公式推导（感觉像是有了实验结果了再给出解释）。此外，权重缩放因子 $s$ 的计算方法还是比较粗糙的，因此，awq 论文进一步优化了 $s$ 的计算法。

2.3 算法-计算缩放因子 s

缩放因子的搜索。

按照前面的分析，我们希望找到权重矩阵通道的每一个缩放系数 $s$，使得量化误差最小，这里 $s$ 如何选择，本质上是优化如下目标函数：

上式 $Q$ 表示权重量化函数（例如，组大小为 128 的 INT3/INT4 量化，以及前文提到的 per-channel INT8 量化），$W$ 是原始 FP16 权重，$X$ 是从小型校准集缓存的输入特征（从预训练数据集中提取了一个小的校准集，以避免过拟合到特定任务）。$s$ 是逐（输入）通道的缩放因子；对于 $s^{-1} \cdot X$，通常可以将其与前一个操作符融合（参见 Wei 等，2022b；Xiao 等，2022， SmoothQuant 源码分析文章也详细解释了）。

按照作者的观点，激活值越大，对应通道越显著，就应该分配更大的缩放系数降低其量化误差。因此，作者统计了各通道的平均激活值（计算输入矩阵各列绝对值的平均值），并直接将此作为各通道的缩放系数。同时引入一个变量 $\alpha$ 用于平衡显著通道和非显著通道的系数，并通过计算不同 $\alpha$ 下的 MSE 损失（$\mathcal{L}$），损失最小的就是最佳的 $\alpha$。转换成公式可得求权重缩放系数 $s$ 的表达式如下所示：

其中 $\text{mean(abs}({\mathbf{x}}))$ 是逐通道计算的激活值绝对值的平均值，$MSE$ 损失是模型网络层的浮点结果和量化结果的均方误差，计算公式为 $\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (out_{fp} - out_{quant})^2$。

另外，在求 $s$ 中需要注意两点：

1. $s$ 计算过程中会按照超参数 group_size 对通道进行分组，每组共享一个 $\alpha$。
2. 码实现和论文有个细节不同，为了防止 $s$ 过大或者过小，作者还进行了一步数据标准化：

for ratio in range(n_grid):
    ratio = ratio * 1 / n_grid
    scales = x_max.pow(ratio).clamp(min=1e-4).view(-1)
    scales = scales / (scales.max() * scales.min()).sqrt()
    ########################## 省略代码#####################

到这里权重缩放系数 $s$ 的计算公式(5) 的意义和细节我们已经彻底搞懂了，但是还有最后一个问题是，$\alpha$ 如何取值呢？作者认为可以通过在区间 $[0, 1]$ 上进行快速网格搜索来找到最佳的 $\alpha$（0 表示不进行缩放；1 表示在搜索空间中最激进的缩放）。但这种方法到底是怎么做的，论文中并没有提。通过阅读源码，发现该方法实际上就是在 [0,1] 区间平均取 20 个数，0, 0.05, 0.10, 0.15 …… 然后逐个计算不同 $\alpha$ 下的 MSE 损失，损失最小的就是最佳的 $\alpha$。得到最佳 $\alpha$ 后，最佳缩放系数 $s$ 也随之确定。

$\alpha$ 和 $s$ 具体取值的实现代码如下所示:

n_grid = 20 # 搜索网格大小, 即取 20 个 alpha 实验值
history = []
org_sd = {k: v.cpu() for k, v in block.state_dict().items()}
for ratio in range(n_grid):
    ratio = ratio * 1 / n_grid
    # 计算缩放因子 s
    scales = x_max.pow(ratio).clamp(min=1e-4).view(-1)
    scales = scales / (scales.max() * scales.min()).sqrt()
    # 缩放并量化全连接层的权重
    for fc in linears2scale:
        fc.weight.mul_(scales.view(1, -1).to(fc.weight.device))
        fc.weight.data = w_quantize_func(fc.weight.data) / (scales.view(1, -1))
    # 获取缩放后的输出
    out = block(x, **kwargs)
    if isinstance(out, tuple):
        out = out[0]

    # 计算 MSE 损失
    loss = ((org_out - out).float().pow(2).mean().item())  # 使用 float 类型防止溢出
    history.append(loss)
    is_best = loss < best_error
    if is_best:
        best_error = loss
        best_ratio = ratio
        best_scales = scales
    # 恢复模块的原始状态
    block.load_state_dict(org_sd)
    # 最佳缩放因子
    best_scales = best_scales.view(-1)

为了验证 AWQ 算法的有效性，作者做了 OPT 模型在 INT3-g128 量化下的消融实验，实验结果显示 AWQ 明显优于 RTN，并实现了和混合精度（1% FP16）相当的精度，同时对硬件更友好。

3. 实验

实验设置：基于 AWQ 算法作者实现了一个极简 llm 推理框架-tinychat，并做了各种性能对比实验，其中关于速度比较的实验结果描述在下面。

实验结果

如图 9(a) 所示，TinyChat 在 4090 显卡上相比 Huggingface FP16 实现，为 Llama-2、MPT 和 Falcon 三大系列的 LLM 提供了 2.7-3.9 倍的加速。

• 对于 Llama-2-7B，通过 FP16 内核融合将推理速度从 52 tokens/s 提升至 62 tokens/s。在更强的 FP16 基线之上，快速量化线性内核为带来了 $3.1$ 倍的额外加速。
• 对于 Falcon-7B，由于官方实现未正确支持推理时的 KV 缓存，其速度明显慢于其他模型。在这种情况下，tinychat 的 FP16 优化实现了 1.6 倍的加速。在配备 8GB 内存的笔记本 4070 显卡上，tinychat 能够以 33 tokens/s 运行 Llama-2-13B，而 FP16 实现无法运行 7B 模型。

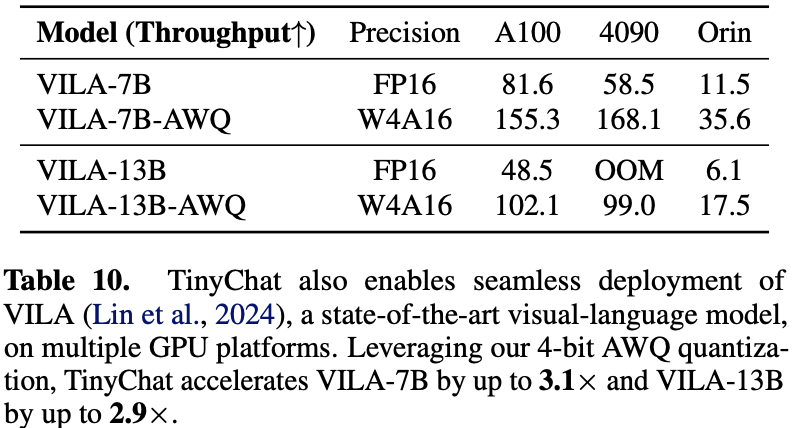
表 10 还展示了视觉-语言模型加速效果。在 NVIDIA Jetson Orin 上，TinyChat 为 VILA-7B 和 VILA-13B 提供了约 $3$ 倍的加速。值得一提的是，所有 AWQ 模型的前向传播均使用原生 PyTorch API 实现，并支持多种 GPU 架构，因此 TinyChat 具备出色的扩展性。

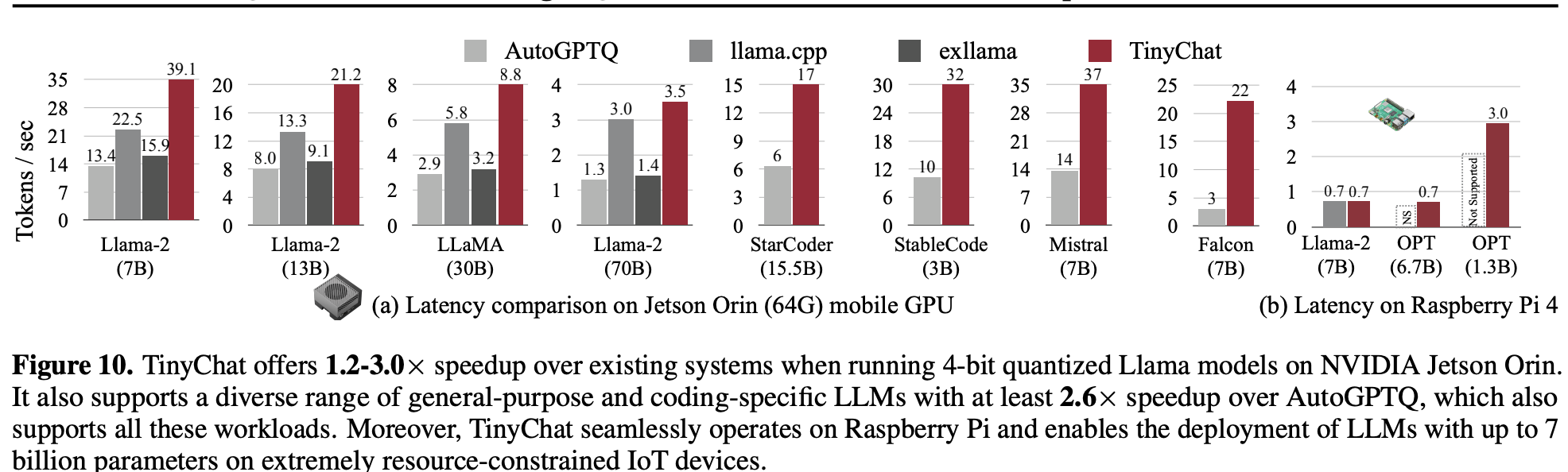
与其他系统的比较。在图 10 中，作者将 TinyChat 与现有的边缘 LLM 推理系统 AutoGPTQ、llama.cpp 和 exllama 进行了对比。在 Orin 上，TinyChat 比 llama.cpp 快最高 1.7 倍。此外，llama.cpp 和 exllama 适应性有限，主要针对 LLaMA 和 Llama-2 模型，而 TinyChat 支持更广泛的应用，包括 StarCoder (Li 等，2023c)、StableCode (GPTNeoX) (Black 等，2022)、Mistral (Jiang 等，2023) 和 Falcon (Penedo 等，2023)，且始终显著快于 AutoGPTQ。TinyChat 甚至在资源极度受限的 Raspberry Pi 4B 上实现了 LLM 部署，7B 模型的速度达到了 0.7 tokens/s。

4. 结论

作者提出的激活感知权重量化 (AWQ)，是一种用于 LLM 低位权重压缩的简便有效方法。基于权重在 LLM 中重要性不均的观察，AWQ 采用逐通道缩放来减少关键权重的量化损失。AWQ 不会对校准集过拟合，并能够保留 LLM 在不同领域和模态中的通用能力。它在语言建模方面优于现有方法，并可应用于指令微调的语言模型和多模态语言模型。和 Huggingface 的 FP16 实现相比，作者实现的 TinyChat 系统进一步将 AWQ 实现的内存节省转化为 $3.2-3.3$ 倍的实际加速效果。另外，AWQ 的提出，使得在树莓派和手机端侧部署大模型成为了可落地的存在。

参考资料

• AWQ: Activation-aware Weight Quantization for LLM Compression and Acceleration
• 深入理解AWQ量化技术
• https://github.com/mit-han-lab/llm-awq