DeepSeekV2 论文解读

Categories: Transformer 2025-02-07

1. 介绍
2. 架构
- 2.1 多头潜变量注意力（MLA）：提升推理效率
- 2.2 DeepSeekMoE：以经济成本训练强大的模型
参考资料

1. 介绍

DeepSeek-V2 是一种高效的开源混合专家（MoE）语言模型，基于创新的 Transformer 架构，实现了经济的训练和高效的推理。DeepSeek-V2 具有 2360 亿个参数(236B)，每个 token 激活 21 亿个参数，支持 128K tokens 的上下文长度。

和 DeepSeekV1 模型结构沿用 llama 结构不同，DeepSeekV2 提出了多头潜在注意力（MLA）和 DeepSeekMoE，旨在优化 Transformer 框架中的注意力模块和前馈网络（FFNs）。

MLA: Multi-head Latent Attention 结构，通过低秩键值联合压缩，减少了推理时的 KV 缓存，从而提高了推理效率。
DeepSeekMoE: FFN（标准 MOE）的优化版。
- 细粒度专家划分(Routed Expert)：相比标准 MOE，DeepSeekMoE 在保持参数量不变的前提下，通过减小每个 Expert 的 FFN 维度，来增加 Expert 数量，进行更细粒度专家划分。
- 共享专家隔离(Shared Expert): 用于表示 Routed Expert 中的共用知识信息，减少 Routed Expert 的知识冗余问题。

DeepSeek-V2 架构图如下所示：

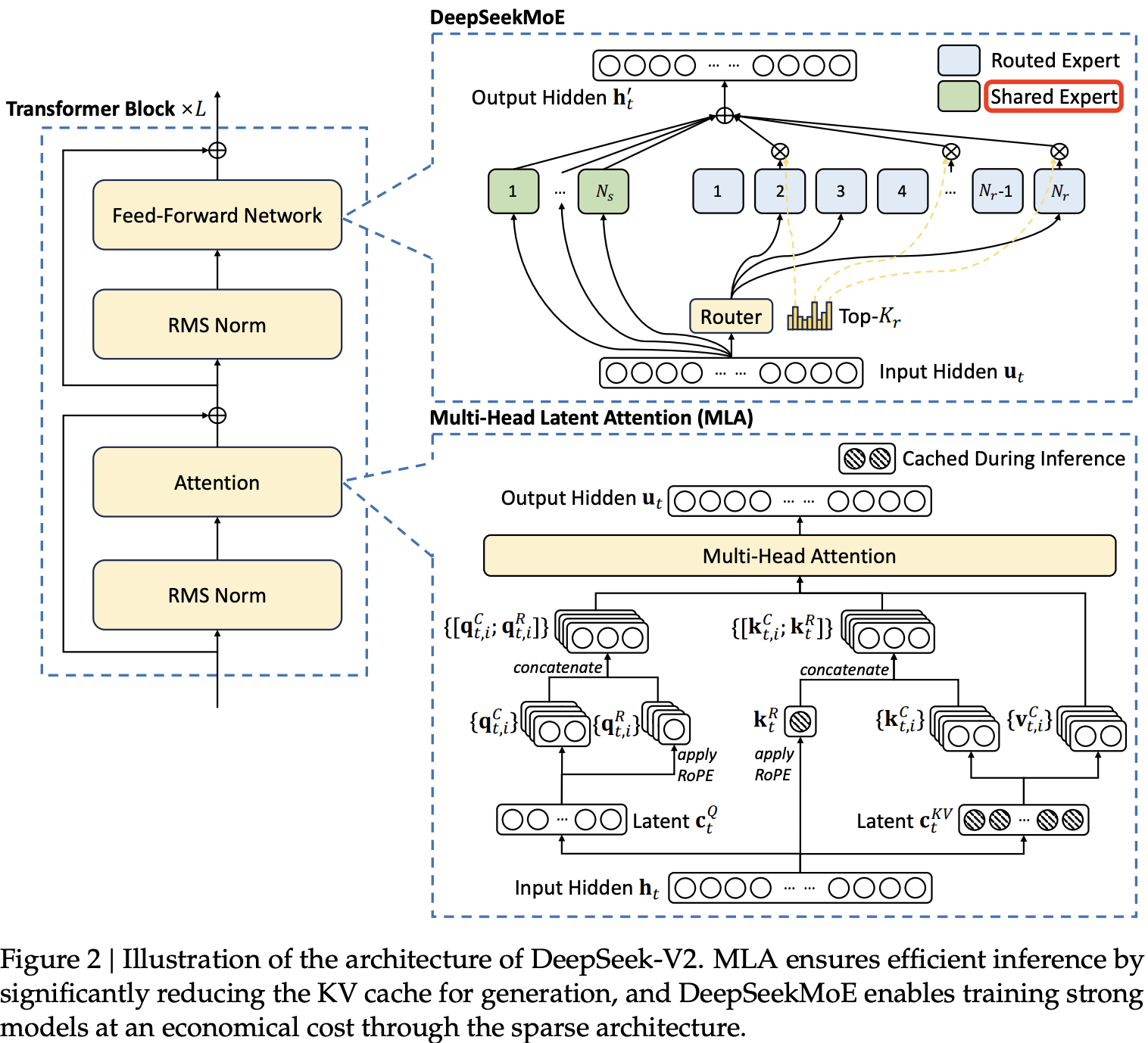
architecture_of_DeepSeekv2

2. 架构

本节介绍 MLA 和 DeepSeekMoE 的详细设计。

2.1 多头潜变量注意力（MLA）：提升推理效率

传统的 Transformer 模型通常采用多头注意力（MHA），但在生成（generation）过程中，其庞大的 Key-Value（KV）缓存会成为限制推理效率的瓶颈。为减少 KV 缓存占用，研究者提出了多查询注意力（MQA）（Shazeer, 2019）和分组查询注意力（GQA）（Ainslie et al., 2023）。这两种方法虽然减少了 KV 缓存需求，但在性能上仍无法与 MHA 相媲美（关于 MHA、GQA 和 MQA 的消融实验见附录 D.1）。

DeepSeek-V2 引入了一种全新的注意力机制多头潜变量注意力（MLA）。MLA 结合了低秩键值联合压缩（low-rank key-value joint compression,），在推理时大幅降低 KV 缓存需求，同时在性能上超越 MHA。

MLA 本质上是通过低秩转换的思路减少 head 的维度，即换为一个压缩的 QKV，存储的KV 的维度显著减小，而不是 GQA 方法减少 kv heads 的数量。

2.1.1 Standard Multi-Head Attention

先回顾下标准的多头注意力（MHA）机制。设 $d$ 为嵌入维度，$n_h$ 为注意力头数，$d_h$ 为单个注意力头的维度，$h_t \in R_d$ 表示第 $t$ 个 token 进入注意力层的输入向量。

在 MHA 机制中，我们通过三个投影矩阵 $W_Q、W_K、W_V \in \mathbb{R}^{n_h d_h\times d}$ 分别计算得到查询向量、键向量和值向量（$q_t、k_t、v_t \in \mathbb{R}^{n_h d_h}$），QKV 向量的线性变换公式如下所示：

QKV 的线性变换的权重矩阵的第二个维度大小一定为嵌入维度 $d$。

\[\mathbf{q}_t = W^Q \mathbf{h}_t, \tag{1}\] \[\mathbf{k}_t = W^K \mathbf{h}_t, \tag{2}\] \[\mathbf{v}_t = W^V \mathbf{h}_t, \tag{3}\]

然后，$q_t$, $k_t$, $v_t$ 将被切分为 $n_h$ 个头（heads），用于多头注意力计算：

\[[\mathbf{q}_{t,1}; \mathbf{q}_{t,2}; \dots; \mathbf{q}_{t,n_h}] = \mathbf{q}_t \tag{4}\] \[[\mathbf{k}_{t,1}; \mathbf{k}_{t,2}; \dots; \mathbf{k}_{t,n_h}] = \mathbf{k}_t \tag{5}\] \[[\mathbf{v}_{t,1}; \mathbf{v}_{t,2}; \dots; \mathbf{v}_{t,n_h}] = \mathbf{v}_t \tag{6}\] \[\mathbf{o}_{t,i} = \sum_{j=1}^{t} \text{Softmax}_j \left( \frac{\mathbf{q}_{t,i}^T \mathbf{k}_{j,i}}{\sqrt{d_h}} \right) \mathbf{v}_{j,i} \tag{7}\] \[\mathbf{u}_t = W^O [\mathbf{o}_{t,1}; \mathbf{o}_{t,2}; \dots; \mathbf{o}_{t,n_h}] \tag{8}\]

其中，$q_{t,i}$, $k_{t,i}$, $v_{t,i} \in \mathbb{R}^{d_h}$ 分别表示第 $i$ 个注意力头的查询（query）、键（key）和值（value）；$W_O \in \mathbb{R}^{d \times d_h n_h}$ 表示输出投影矩阵。在推理过程中，key 和 value 需要被缓存，以加速计算，避免重复计算。

标准 MHA 每个 token 的 kv 缓冲大小 = $2n_hd_h l$，单位为字节 byte；如果使用了 GQA 优化技术，每个 token 的 kv 缓冲大小变为 $2n_{kv}d_h l = 2n_hd_h l/\text{groups}$ 个元素。下标 $t$ 表示第几个 token，下标 $[1, n_h]$ 表示注意力头数，$l$ 表示 decoder layers 数目。

在模型部署时，这种庞大的 KV 缓存成为了一个主要的瓶颈，限制了最大批量大小（batch size）和序列长度（sequence length）。

2.1.2 Low-Rank Key-Value Joint Compression

MLA 的核心是对键（keys）和值（values）进行低秩联合压缩（low-rank joint compression），以减少 KV 缓存（KV cache）的占用：

\[\mathbf{c}_t^{KV} = W^{DKV} \mathbf{h}_t, \tag{9}\] \[\mathbf{k}_t^{C} = W^{UK} \mathbf{c}_t^{KV}, \tag{10}\] \[\mathbf{v}_t^{C} = W^{UV} \mathbf{c}_t^{KV}, \tag{11}\]

KV 向量的生成是先投影到一个低维（5120 -> 512）的 compressed_kv 向量（$\mathbf{c}_t^{KV}$）再升维展开得到 $\mathbf{k}_t^{C}$ 和 $\mathbf{v}_t^{C}$。上述公式的各个变量定义：

$\mathbf{c}_t^{KV}$ 是 keys 和 values 的压缩后的潜在向量（latent vector）；
$d_c (\ll d_h n_h)$ 代表 KV 压缩维度（KV compression dimension）
$W^{DKV} \in \mathbb{R}^{d_c \times d}$ 是降维投影矩阵（down-projection matrix）；
$W^{UK}, W^{UV} \in \mathbb{R}^{d_h n_h \times d_c}$ 分别是 keys 和 values 的升维投影矩阵（up-projection matrices）。

另外，虽然不能减少 KV Cache 的占用，但是为了减少训练时的激活内存（activation memory），同样也对查询（queries）也进行了低秩压缩（low-rank compression）。同样也是先投影到一个低维（5120 -> 1536）的 compressed_kv 向量（$\mathbf{c}_t^{Q}$）再升维展开得到 $\mathbf{q}_t^{C}$:

\[\mathbf{c}_t^{Q} = W^{DQ} \mathbf{h}_t, \tag{12}\] \[\mathbf{q}_t^{C} = W^{UQ} \mathbf{c}_t^{Q}, \tag{13}\]

类比前面的公式可知:

$\mathbf{c}_t^{Q} \in \mathbb{R}^{d’_c}$ 是查询的压缩潜在向量（compressed latent vector for queries）；
$d’_c (\ll d_h n_h)$ 表示查询的压缩维度（query compression dimension）；
$W^{DQ} \in \mathbb{R}^{d’_c \times d}$ 是查询的降维投影矩阵；
$W^{UQ} \in \mathbb{R}^{d_h n_h \times d’_c}$ 是查询的升维投影矩阵（up-projection matrix）。

2.1.3 Decoupled Rotary Position Embedding

和 DeepSeek 67B（DeepSeek-AI, 2024）类似，作者也计划在 DeepSeek-V2 中使用旋转位置编码（RoPE, Rotary Position Embedding）（Su et al., 2024）。但是，RoPE 与低秩 KV 压缩（low-rank KV compression）并不兼容。

具体来说，RoPE 使键（Key）和查询（Query）都具备位置敏感性（position sensitivity）。如果我们在压缩后的键 $\mathbf{k}_t^{C}$ 上应用 ROPE，那么实际上我们得到的键表示会是这样的形式：

\[k_t^R = \text{ROPE}(W^{UK} \mathbf{c}_t^{KV})\]

很明显式（10）中的 $W^{UK}$ 和 RoPE 旋转矩阵在计算过程中“耦合”在一起—这意味着 $W^{UK}$ 输出的结果会始终被那个依赖于具体位置的旋转矩阵所“修正”或“调制”。

这样会导致在执行 atten weight（$QK^T$）的计算优化中，无法像原本设想的那样，把 $W^{UK}$ 吸收到 $W^Q$ 中，因为当前生成 token 相关的 RoPE 矩阵位于 $W^Q$ 和 $W^{UK}$ 之间，而矩阵乘法不满足交换律（commutative law）。这直接导致在推理过程中，我们必须重新计算所有 prefix token 的键（keys），这将显著降低推理效率。

为了解决这个问题，作者提出了一种解耦 RoPE（decoupled RoPE）的策略，通过额外引入多头查询（multi-head queries）$q_{t,i}^R \in \mathbb{R}^{d^R_h}$和采用一个共享键（shared key) $k_t^R \in \mathbb{R}^{d^R_h}$ 来承载 RoPE 信息。其中 $d^R_h$ 代表解耦查询和键的每头维度（per-head dimension of the decoupled queries and key）。

在使用解耦 RoPE 策略后，MLA 的计算过程变成如下所示：

\[\left[ \mathbf{q}_{t,1}^{R}; \mathbf{q}_{t,2}^{R}; \dots; \mathbf{q}_{t,n_h}^{R} \right] = \mathbf{q}_t^{R} = \text{RoPE}(W^{QR} \mathbf{c}_t^{Q}), \tag{14}\] \[\mathbf{k}_t^{R} = \text{RoPE}(W^{KR} \mathbf{h}_t), \tag{15}\] \[\mathbf{q}_{t,i} = \left[ \mathbf{q}_{t,i}^{C}; \mathbf{q}_{t,i}^{R} \right], \tag{16}\] \[\mathbf{k}_{t,i} = \left[ \mathbf{k}_{t,i}^{C}; \mathbf{k}_{t,i}^{R} \right], \tag{17}\] \[\mathbf{o}_{t,i} = \sum_{j=1}^{t} \text{Softmax}_j \left( \frac{\mathbf{q}_{t,i}^{T} \mathbf{k}_{j,i}}{\sqrt{d_h + d_h^{R}}} \right) \mathbf{v}_{j,i}^{C}, \tag{18}\] \[\mathbf{u}_t = W^{O} \left[ \mathbf{o}_{t,1}; \mathbf{o}_{t,2}; \dots; \mathbf{o}_{t,n_h} \right], \tag{19}\]

其中:

$W^{QR} \in \mathbb{R}^{d^R_h n_h \times d’_c}$ 表示生成解耦查询（decoupled queries）矩阵
$W^{KR} \in \mathbb{R}^{d^R_h \times d}$ 表示解耦键（decoupled key）的矩阵。
$\text{RoPE}(\cdot)$ 表示应用 RoPE 矩阵的操作;
$\cdot ; \cdot$ 表示拼接（concatenation）操作。

在推理过程中，解耦后的键（decoupled key）也需要缓存。因此，DeepSeek-V2 的 KV 缓存总大小为 $(d_c + d^R_h)l$ 个元素。

很明显和前面公式相比，多了 $\mathbf{q}_t^{R}$ 和 $\mathbf{k}_t^{R}$ 两个变量的计算过程，它们用于单独承载 ROPE 信息，并和前面计算得到的 $\mathbf{q}_t^{C}$ 和 $\mathbf{k}_t^{C}$ 做拼接后得到新的 $q、k$，再执行 atten weight 计算（$qk^t$）。

最后，总结下完成的 MLA 计算过程如下所示：

MLA 结构的可视化图如下所示：

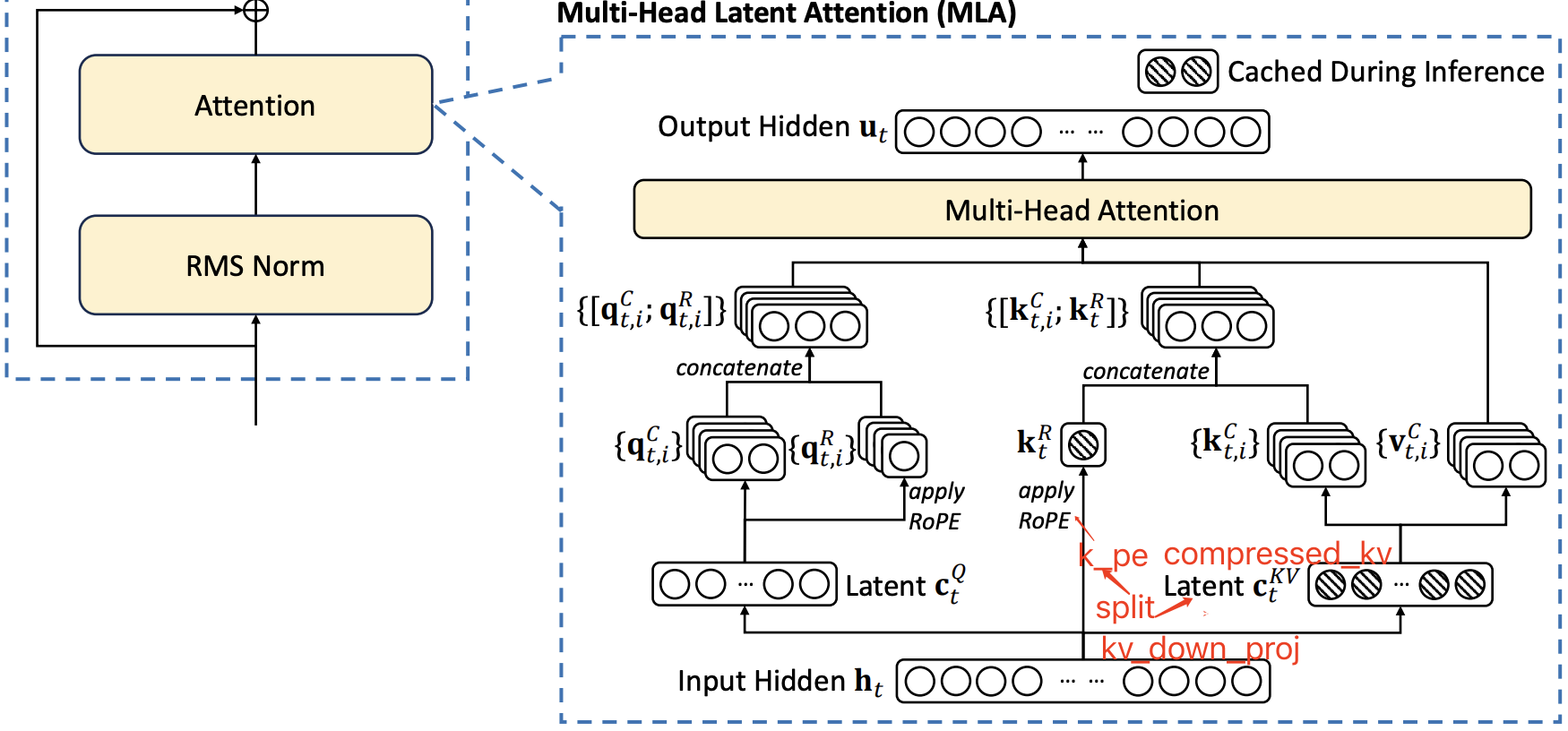
2.1.4 kv cache 大小的比较

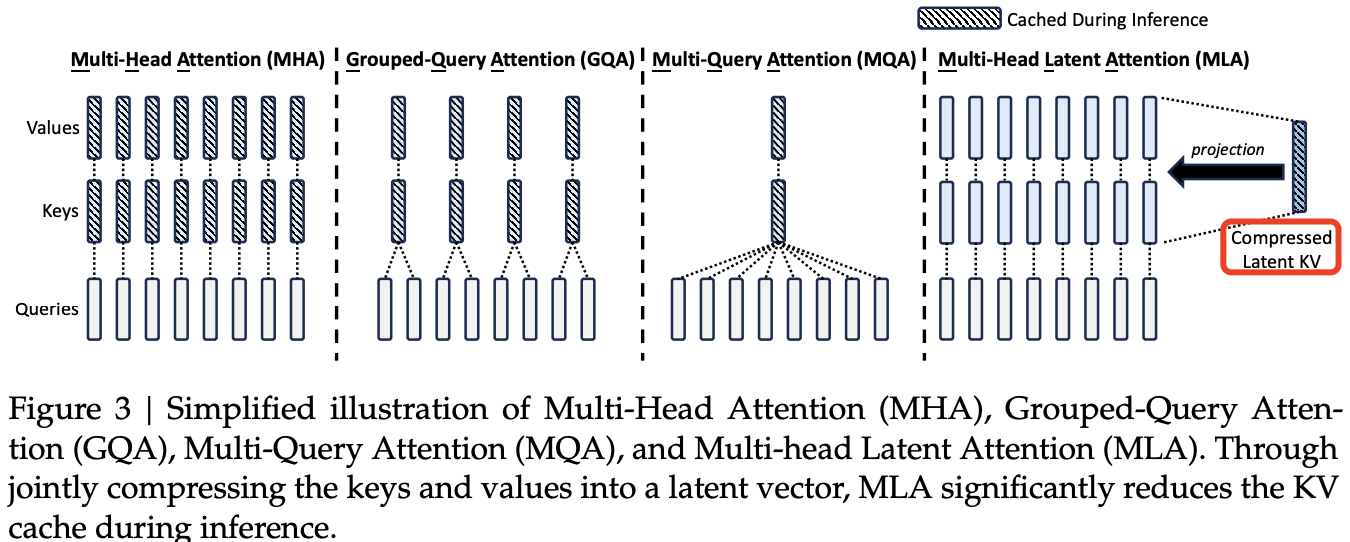
多头注意力（MHA）、分组查询注意力（GQA）、多查询注意力（MQA）和多头潜在注意力（MLA）的简化示意图对比如下图 3 所示。通过将键（Key）和值（Value）压缩到一个潜在向量中，MLA 在推理时大幅减少了对 KV 缓存的需求。

下表 1 中对比了不同注意力机制下，每个 token 需要的 KV 缓存大小。MLA 仅需要少量的 KV 缓存，其大小相当于仅有 $2.25$ 组（groups）的 GQA，但其性能却强于 MHA。

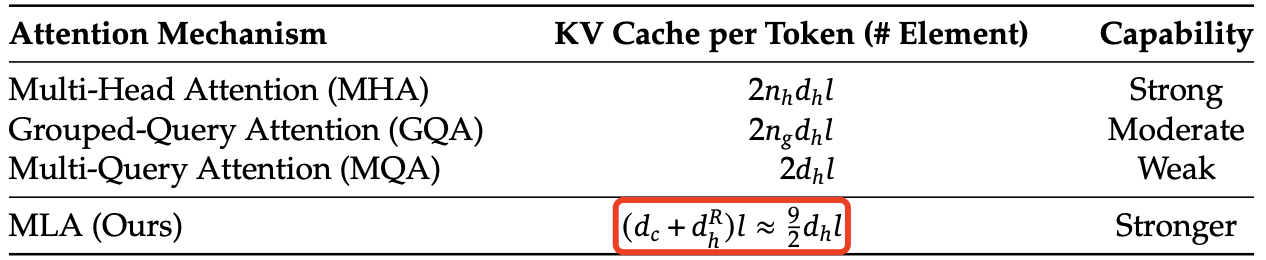
table1

表 1｜不同注意力机制下，每个 token 需要的 KV 缓存对比。其中，

$n_h$ 表示注意力头的数量，
$d_h$ 表示每个注意力头的维度，
$l$ 表示模型层数，
$n_g$ 表示 GQA 的组数，
$d_c$ 和 $d^R_h$ 分别表示 MLA 中的 KV 压缩维度和解耦查询与键的 per-head 维度。

KV 缓存的数量以元素(elements)个数计算，不考虑存储精度（storage precision）。对于 DeepSeek-V2，

$d_c$ 设定为 $4d_h$。
$d^R_h$ 设定为 $\frac{d_h}{2}$。

因此，DeepSeek-V2 只需要相当于 GQA $2.25$ 组的 KV 缓存，但相比 MHA 仍能提供更强的性能。

2.1.5 总结

MLA 虽然增大了计算量，但 KV Cache 的减少也降低了显存和带宽的压力，且 llm 推理的 decode 阶段是受限于带宽瓶颈和显存瓶颈，因此 MLA 的引入理论上能明显提高 Generation 的速度。

2.2 DeepSeekMoE：以经济成本训练强大的模型

对于 FFN（前馈网络），我们采用 DeepSeekMoE 架构（Dai et al., 2024）。DeepSeekMoE 主要包含两个关键思想：

更精细地划分专家网络，提升每个专家的专业性，提高知识表达的准确度。
引入部分共享专家，减少不同专家间的知识冗余，从而提升计算效率。

相比传统的 MoE 架构（如 GShard，Lepikhin et al., 2021），DeepSeekMoE 在相同的专家参数量和激活参数量下，能显著提升模型性能。

设 $u_t$ 为第 $t$ 个 token 的 FFN 输入，其 FFN 输出 $h’_t$ 计算如下：

\[\mathbf{h}_t' = \mathbf{u}_t + \sum_{i=1}^{N_s} \text{FFN}_i^{(s)} (\mathbf{u}_t) + \sum_{i=1}^{N_r} g_{ij,t} \text{FFN}_i^{(r)} (\mathbf{u}_t), \tag{20}\] \[g_{ij,t} = \begin{cases} s_{ij,t}, & s_{ij,t} \in \text{Topk}(\{s_{ij,t}| 1 \leq j \leq N_r\}, K_r), \\ 0, & \text{otherwise}, \end{cases} \tag{21}\] \[s_{ij,t} = \text{Softmax}_i (\mathbf{u}_t^T e_i), \tag{22}\]

上述公式中：

$N_s$ 和 $N_r$ 分别表示共享专家和路由专家的数量；
$FFN(s) i(·)$ 和 $FFN(r) 𝑖(·)$ 分别表示第 $i$ 个共享专家和第 $i$ 个路由专家的计算过程；
$K_r$ 表示激活的路由专家数量；
$g_{i, t}$ 是第 $i$ 个专家的门控值，用来决定该专家是否激活；
$s_{i, t}$ 是 token 到专家的亲和度值，表示 token 和专家之间的相关性；
$e_i$ 是该层第 $i$ 个路由专家的质心，用于表示专家的聚合特征；
$\text{Topk}(·, K)$ 表示从第 $t$ 个 token 计算的所有路由专家的亲和度分数中，选择出 $K$ 个最高的值，并将这些分数组成一个集合。

2.2.2. 设备受限路由（Device-Limited Routing）

作者设计了一种设备受限的路由机制，用于限制 MoE 相关的通信成本。

当采用专家并行（expert parallelism）时，路由专家（routed experts）会分布在多个设备上。对于每个 token，它的 MoE 相关通信频率与其目标专家所涉及的设备数量成正比。由于 DeepSeekMoE 采用了精细的专家划分策略，激活的专家数量可能较多，如果直接应用专家并行，会导致更高的 MoE 相关通信成本。

在 DeepSeek-V2 中，除了直接选择得分最高的 $K$ 个路由专家（top-K selection）之外，我们还确保每个 token 的目标专家最多分布在 $M$ 台设备上。具体而言，对于每个 token，我们首先选择拥有最高亲和度分数的 $M$ 台设备，然后在这 $M$ 台设备上的专家中执行 top-K 选择。实践中，我们发现当 $M \geq 3$ 时，设备受限路由的效果可以大致匹配不受限的 top-K 路由。

2.2.3. 负载均衡的辅助损失（Auxiliary Loss for Load Balance）

作者在自动学习的路由策略中引入了负载均衡机制。

负载不均衡会导致路由塌陷（routing collapse）（Shazeer et al., 2017），即部分专家可能无法得到充分训练和利用。
在专家并行（expert parallelism）机制下，负载不均衡会降低计算效率。

在 DeepSeek-V2 训练过程中，我们设计了三种辅助损失（auxiliary losses），分别用于控制：

专家级负载均衡（ $L_{\text{ExpBal}}$ ），
设备级负载均衡（ $L_{\text{DevBal}}$ ），
通信均衡（ $L_{\text{CommBal}}$ ）。

这三种损失函数协同作用，确保 DeepSeek-V2 在计算资源受限的条件下，仍能高效训练高性能 MoE 模型。

2.2.4. Token-Dropping 策略

虽然平衡损失有助于实现负载平衡，但它无法完全保证负载的严格平衡。为了解决负载不平衡带来的计算浪费，作者在训练中引入了设备级的 Token-Dropping 策略。该策略首先计算每个设备的平均计算预算，将每个设备的容量因子设为 1.0。然后，借鉴 Riquelme 等人（2021）的思路，我们会丢弃每个设备上亲和度最低的 token，直到达成计算预算。此外，我们还确保约 10% 的训练序列中的 token 不会被丢弃。这样，在推理过程中，我们可以灵活地根据效率需求选择是否丢弃 token，同时保持训练和推理的一致性。

参考资料

你觉得有收获吗？❤️